ML não é uma coisa incompreensível. Não funciona pra todos os casos e não vai necessariamente te oferecer uma solução melhor do que uma implementação bem pensada e deterministica num passe de mágica. Tem as suas utilidades. Podemos resolver problemas de uma forma relativamente simples em ambientes dinâmicos e confusos, ou onde não podemos fazer grandes suposições em relação ao seu funcionamento.
Esse notebook explica um pouco sobre modelos lineares: como eles funcionam e como utilizá-los de forma eficiente. Espero que seja instrutivo e clareie um pouco do tópico pra todo mundo.
Suponha que você é um dev em uma empresa de e-commerce de roupas e calçados. Ao longo dos meses de operação, a equipe coletou amostras para construir uma tabela que mapeia os tamanhos das peças para a altura média das pessoas que as compram, além de informações sobre sexo e tamanho dos sapatos dos compradores.
A fim de fomentar o espirito consumista de seus clientes e impulsionar o ecosistema de blogueirinhas, você deseja recomendar belos calçados após cada compra de roupa. Naturalmente, você deseja recomendar somente os calçados que provavelmente servirão ao cliente específico.
import os
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
from IPython.display import display_html
def display_side_by_side(*args):
html_str=''
for df in args:
html_str+=df.to_html()
display_html(html_str.replace('table','table style="display:inline"'),raw=True)
sns.set()
Coletando as informações
Seus colegas disponibilizaram todos os dados necessários em um arquivo wo_men.csv (o conjunto de dados wo-man, na verdade), para leitura imediata:
DATA_FILE = '/content/drive/Shareddrives/datasets/shoes.csv'
TRUSTED_FILE = '/content/drive/Shareddrives/datasets/shoes.trusted.csv'
x = (pd.read_csv(DATA_FILE)
.drop(columns=['time'])
.dropna())
Não precisamos da coluna de tempo, então podemos ler o arquivo e imediatamente removê-la. Apagamos também as linhas que contém valores faltantes. Procedemos então à exibir:
x.head().round() # as cinco primeiras linhas do conjunto
| sex | height | shoe_size | |
|---|---|---|---|
| 0 | woman | 160.0 | 40.0 |
| 1 | woman | 171.0 | 39.0 |
| 2 | woman | 174.0 | 39.0 |
| 3 | woman | 176.0 | 40.0 |
| 4 | man | 195.0 | 46.0 |
x.describe().round().T # estatísticas gerais sobre as colunas numéricas do conjunto
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| height | 100.0 | 165.0 | 40.0 | 2.0 | 163.0 | 168.0 | 174.0 | 364.0 |
| shoe_size | 100.0 | 40.0 | 6.0 | 35.0 | 38.0 | 39.0 | 40.0 | 88.0 |
x.groupby('sex').count() # a contagem de amostras para cada grupo da variável `sex`.
| height | shoe_size | |
|---|---|---|
| sex | ||
| man | 18 | 18 |
| woman | 82 | 82 |
Observe que há muito mais amostras “woman” que “man”. Isso pode criar um problema depois dependendo da tarefa a ser resolvida e o quão dependente ela é de data-balancing para performar corretamente.
De qualquer forma, vamos primeiro nos preocupar em pre-processar esses dados.
Data Engineering & Análise
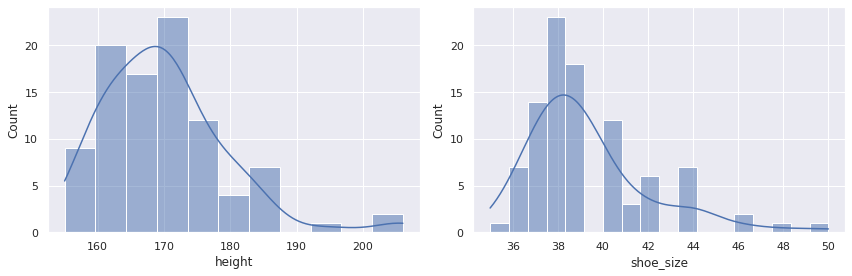
Pra tomarmos (ou para a máquina tomar) decisões precisas, precisamos garantir que estes dados estejam o mais limpo possível. Como as colunas são estruturadas, podemos plotar alguns gráficos para explorá-las:
with sns.axes_style('darkgrid'):
plt.figure(figsize=(16, 4))
plt.subplot(121)
sns.histplot(x.height, kde=True)
plt.subplot(122)
sns.histplot(x.shoe_size, kde=True);
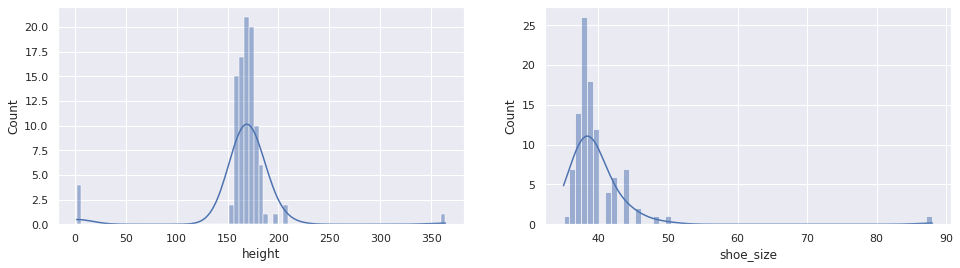
Algo esquisito está acontecendo:
- 0.5% dos usuários tem a altura igual à $0$
- alguns usuários possuem uma altura maior que $350cm$
- alguns usuários calçam sapatos de tamanho próximo à 90
Só pode ser um erro de entrada. Vamos visualizá-los separadamente:
x[x.height < 40]
| sex | height | shoe_size | |
|---|---|---|---|
| 47 | woman | 1.84 | 41.0 |
| 61 | woman | 1.63 | 38.0 |
| 77 | woman | 1.68 | 38.0 |
| 80 | woman | 1.73 | 38.0 |
Claramente, a altura foi escrita em metros em vez de centímetros.
x[x.height > 300]
| sex | height | shoe_size | |
|---|---|---|---|
| 67 | woman | 364.0 | 88.0 |
Isso parece um erro irrecuperável. É melhor removermos essa linha completamente.
def preprocessing(df):
y = df.copy()
y = handle_heights_in_cm(y)
y = drop_illegal_heights(y)
y = drop_illegal_shoe_sizes(y)
return y
def drop_illegal_heights(df):
# Numbers based on the world-records
# for shortest and tallest person.
return df[(62.8 <= df.height) & (df.height <= 288)]
def handle_heights_in_cm(df):
df[df.height <= 2.88] *= 100
return df
def drop_illegal_shoe_sizes(df):
return df[df.shoe_size <= 75]
x = preprocessing(x)
plt.figure(figsize=(12, 4))
plt.subplot(121)
sns.histplot(x.height, kde=True)
plt.subplot(122)
sns.histplot(x.shoe_size, kde=True)
plt.tight_layout();
plt.figure()
plt.subplot(121)
sns.boxplot(data=x, x='sex', y='height')
plt.subplot(122)
sns.boxplot(data=x, x='sex', y='shoe_size')
plt.tight_layout();
# Pair Plot between all Features in Shoes
plt.figure()
sns.pairplot(data=x, hue='sex')
plt.tight_layout();
Isso significa que há uma clara distinção entre as alturas/tam. dos calçados de homens e mulheres, e eles podem ser variáveis importantes na hora de inferir a qual categoria uma amostra pertence.
x.to_csv(TRUSTED_FILE, index=False)
Estimando o tamanho do calçado a partir da altura
S: existe uma função $f^\star$ que descreve perfeitamente o relacionamento entre tam. calçado à outros atributos físicos, comportamentais e culturais de uma pessoa. Essa função com certeza depende de mais variáveis do que simplesmente a altura.
Q: Podemos aproximar $f^\star$ tal que o erro mínimo associado $E$ é aceitável?
S = x.shoe_size.min(), x.shoe_size.max()
S
(35.0, 50.0)
Podemos definir um estimador (determinístico) que diz diretamente qual é o valor para cada pessoa:
def f(h):
return 36
_, h, s = x.iloc[0]
p = f(h)
E = np.abs(s - p)
s, p, E
(40.0, 36, 4.0)
Considerando uma das amostras do conjunto (a primeira), é possível medir (baseado em alguma função de erro) o quão distante estamos da saída desejada (o tam. do calçado verdadeiro). Erros grandes significam maiores distancias para o valor desejado, enquanto erros baixos implicam em estimadores mais acurados. Vamos chamar a função que usamos acima absolute error function:
\[E(h, s) = |s - f(h)|\]Mas considerar somente a primeira amostra é representativo o suficiente? Construir modelos genéricos baseados em uma única observação é muito selvagem. É melhor olharamos pra todo o conjunto de dados:
def predict(x, fn):
x = x.copy()
x['predicted'] = [fn(h) for h in x.height]
x['error'] = np.abs(x.predicted - x.shoe_size)
return x
predict(x, f).head().round(2)
| sex | height | shoe_size | predicted | error | |
|---|---|---|---|---|---|
| 0 | woman | 160.0 | 40.0 | 36 | 4.0 |
| 1 | woman | 171.0 | 39.0 | 36 | 3.0 |
| 2 | woman | 174.0 | 39.0 | 36 | 3.0 |
| 3 | woman | 176.0 | 40.0 | 36 | 4.0 |
| 4 | man | 195.0 | 46.0 | 36 | 10.0 |
Se calcularmos a média entre todos os absolute errors (alcançando a função MAE), se torna claro que nossas “predições” estão fora do esperado por mais ou menos $3.33$:
predict(x, f).describe().round(2)
| height | shoe_size | predicted | error | |
|---|---|---|---|---|
| count | 95.00 | 95.00 | 95.0 | 95.00 |
| mean | 170.03 | 39.31 | 36.0 | 3.33 |
| std | 9.41 | 2.73 | 0.0 | 2.70 |
| min | 155.00 | 35.00 | 36.0 | 0.00 |
| 25% | 163.00 | 38.00 | 36.0 | 2.00 |
| 50% | 169.00 | 39.00 | 36.0 | 3.00 |
| 75% | 174.50 | 40.00 | 36.0 | 4.00 |
| max | 206.00 | 50.00 | 36.0 | 14.00 |
Observando a tabela acima, a função pode ser trivialmente ajustada para reduzir o erro para $2$. Consegue imaginar como? Pensa um pouquinho antes de exibir o código abaixo.
def f(h):
return 39.31 # populational mean
predict(x, f).describe().round(2)
| height | shoe_size | predicted | error | |
|---|---|---|---|---|
| count | 95.00 | 95.00 | 95.00 | 95.00 |
| mean | 170.03 | 39.31 | 39.31 | 2.00 |
| std | 9.41 | 2.73 | 0.00 | 1.84 |
| min | 155.00 | 35.00 | 39.31 | 0.31 |
| 25% | 163.00 | 38.00 | 39.31 | 0.69 |
| 50% | 169.00 | 39.00 | 39.31 | 1.31 |
| 75% | 174.50 | 40.00 | 39.31 | 2.69 |
| max | 206.00 | 50.00 | 39.31 | 10.69 |
A média populacional é o valor que produz o menor MAE, pela definição de esperança e como a MAE é definida, mas a média dos erros é suficiente pra descrever como está o nosso modelo?
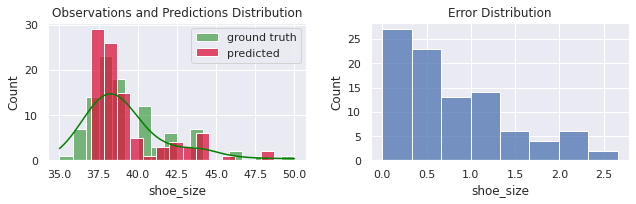
As distribuições de tam. de calçados verdadeira (normalmente chamada de ground truth) e das nossas predições podem oferecer um pouco mais de contexto:
from sklearn import metrics
def evaluate(y, p):
print('MSE =', metrics.mean_squared_error(y, p).round(3))
print('MAE =', metrics.mean_absolute_error(y, p).round(3))
print('R² =', metrics.r2_score(y, p).round(3))
plt.figure(figsize=(9, 3))
plt.subplot(121)
plt.title('Observations and Predictions Distribution')
sns.histplot(y, label='ground truth', kde=True, color='green')
sns.histplot(p, label='predicted', color='crimson')
plt.legend()
plt.subplot(122)
plt.title('Error Distribution')
sns.histplot(np.abs(y - p), label='error')
plt.tight_layout()
p = predict(x, f)
evaluate(p.shoe_size, p.predicted)
MSE = 7.359
MAE = 2.001
R² = -0.0
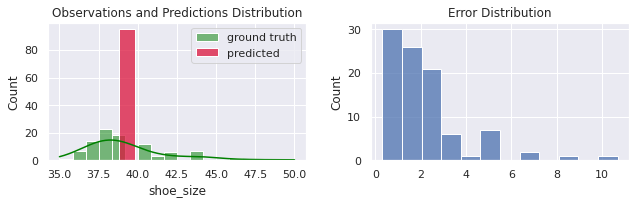
Note que nunca iremos predizer bem para pessoas que possuem o tam. do calçado diferente da média (todo mundo, de acordo com o gráfico abaixo). O segundo gráfico ilustra a partir de uma sequência de diferenças entre valores preditos e variáveis alvo. A maioria dos erros de concentram abaixo de 2 ou 3 números.
O que aconteceria se colocassemos um pouco de variação no nosso modelo? O erro iria aumentar ou diminuir?
def f(h):
return 39.31 + np.random.randn() * 1.84
predict(x, f).describe().round(2)
| height | shoe_size | predicted | error | |
|---|---|---|---|---|
| count | 95.00 | 95.00 | 95.00 | 95.00 |
| mean | 170.03 | 39.31 | 39.00 | 2.37 |
| std | 9.41 | 2.73 | 1.81 | 2.21 |
| min | 155.00 | 35.00 | 35.61 | 0.03 |
| 25% | 163.00 | 38.00 | 37.68 | 0.72 |
| 50% | 169.00 | 39.00 | 39.16 | 1.83 |
| 75% | 174.50 | 40.00 | 40.20 | 3.49 |
| max | 206.00 | 50.00 | 44.08 | 14.33 |
O erro médio subiu um pouco, mas não tenho certeza se isso é significativo. As distribuições, entretanto, estão muito mais parecidas:
p = predict(x, f)
evaluate(p.shoe_size, p.predicted)
MSE = 9.372
MAE = 2.431
R² = -0.274
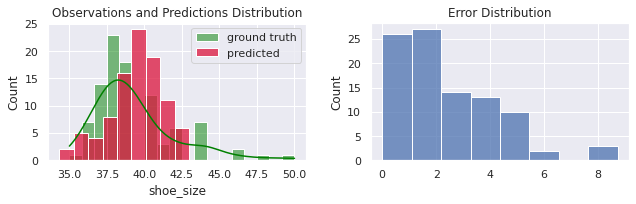
Nós ainda estamos muito ruins (pior do que antes) em predizer a variável de interesse para pessoas com pés anormais, mas agora podemos fingir que o nosso modelo é inteligente (ou ao menos não determinístico).
O segundo gráfico nos diz que ainda estamos fazendo mais erros pequenos do que grandes, mas que no geral mais erros grandes acontecem agora que adicionamos o fator aleatório np.random.randn.
Os modelos acima utilizam informações estatísticas para criar uma resposta. Isso seria argumentavelmente uma decisão “racional”, mas isso seria considerado “machine learning”?
Aprendendo parâmetros
Como podemos melhorar ainda mais nossas estimativas? Até agora, nós temos uma função estimadora constante e uma função de cálculo de erro. A próxima função mais simples é a função linear:
\[f(x) = ax + b\]Estudo sobre variáveis
def f(h, a, b):
return a*h + b
Essa função assume vários comportamentos dependendo dos parâmetros $a$ e $b$:
with sns.axes_style('darkgrid'):
sns.scatterplot(data=x, x='height', y='shoe_size',
hue='sex',
label='real data')
for a, b in ((.08, 17),
(.25, 0),
(.07, 20)):
h = 150 + np.arange(80)
p = f(h, a, b)
sns.lineplot(x=h, y=p, label=f'f={a:.2f}x + {b:.1f}')
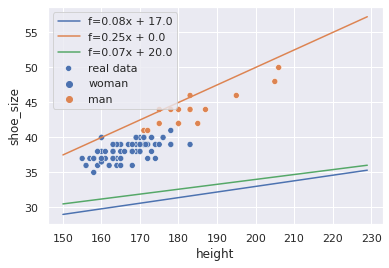
Existe uma linha $(a, b)$ que estima perfeitamente a variável alvo em cima da característica de entrada? Pela figura, com certeza não: as amostras não são colineares. Qual é a melhor linha então?
Se todas as $n$ amostras têm a mesma importância, então nós queremos estimar todas elas o melhor possível. Com MAE como função de erro, podemos escolher parâmetros $a, b$ tais que essa métrica atinja um valor mínimo.
Em outras outras palavras:
Onde $f_i = ah_i + b$.
Só que existe um problema aqui: a função norma não é suave e imediatamente diferenciável:
def mae_loss(y, p):
return np.abs(y - p).mean()
p = np.arange(101) -50
sns.lineplot(x=p, y=np.abs(p));
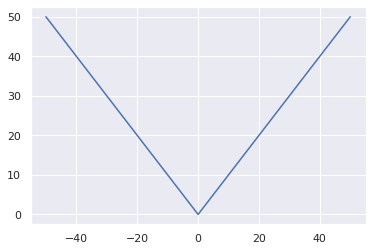
Isso não é exatamente um problema nesse caso onde uma única variável está sendo otimizada, mas causa a criação de muitos pontos não-diferenciaveis em problemas que dependem de múltiplas características, o que torna o processo de otimização instável.
Proposta: porque não substituímos pela função de otimização quadrática? Isso irá curvar a linha próximo ao 0. O modelo então se torna:
\[argmin_{a, b} \frac{1}{n}\sum_i^{n} (y_i - p_i)^2\]Essa função é diferenciável.
def mse_loss(y, p):
return ((y - p) ** 2).mean()
p = np.arange(101) -50
sns.lineplot(x=p, y=p ** 2);
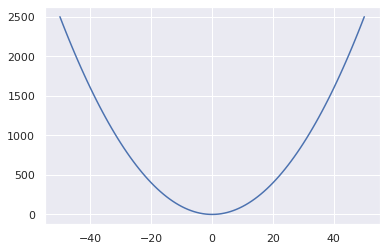
Mas é claro, nós temos dois parâmetros, então o nosso espaço de busca se parece muito mais com isso:
As = np.linspace(-10, 10, 40)
Bs = np.linspace(-1000, 1000, 100)
# Generate many combinations of (a, b)
aa, bb = np.meshgrid(As, Bs)
ab = np.asarray([aa.ravel(), bb.ravel()]).T
# Compute the loss for each combination
mse = [mse_loss(x.shoe_size, f(x.height, a, b))
for a, b in ab]
space = np.hstack((ab, np.asarray(mse).reshape(-1, 1)))
ax = plt.gca(projection='3d')
ax.plot_trisurf(space[:, 0], space[:, 1], space[:, 2], color=(0, 0, 0, .1), edgecolor='orange')
ax.set_xlabel('a'), ax.set_ylabel('b'), ax.set_zlabel('MSE')
ax.view_init(30, -50)
plt.tight_layout();
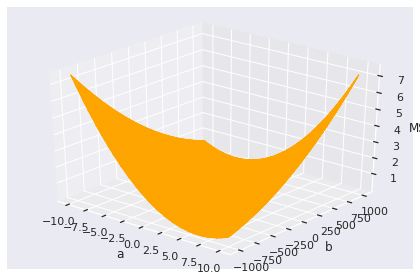
De qualquer forma, para propósito de ilustração, vamos voltar ao nosso cenário com uma única variável (suponha $b = 0$) a ser refinada. Podemos começar em um ponto aleatório no espaço:
a0 = 1 + .25 * np.random.randn()
b0 = 0
f0 = f(x.height[0], a0, b0)
mse0 = mse_loss(x.shoe_size, f(x.height, a0, b0))
print(f'{a0:.3f}, {b0:.3f}, {f0:.3f}, {mse0:.3f}')
0.488, 0.000, 78.148, 1919.643
def point_on_curve(e, a, b):
plt.plot([a], [e], 'o')
plt.annotate(f'mse(${a:.3f}h + {b:.3f})$',
xy=(a, e),
xytext=(a + .1, e));
As = np.linspace(-2, 2, 20)
mses = [mse_loss(x.shoe_size, f(x.height, ax, b0)) for ax in As]
plt.figure(figsize=(5, 3))
sns.lineplot(x=As, y=mses)
point_on_curve(mse0, a0, b0)
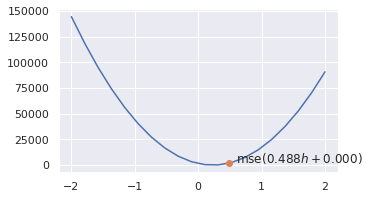
Solução exata da equação
Se $a$ crescer, o mse aumenta quadraticamente.
O ponto ótimo $a\star$ é no intervalo $(0, 1)$, tal que o mse é mínimo. Um modelo ótimo é então definido por:
Essa equação só tem um ponto crítico, então tem solução imediata $\frac{\partial mse}{\partial a} = 0$. Expandindo essa derivada:
\[\begin{align*} \frac{\partial}{\partial a} \frac{1}{n}\sum_i (y_i -ah_i -b)^2 &= \frac{1}{n}\sum_i \frac{\partial mse}{\partial a} (y_i - ah_i -b)^2 \\ &= \frac{2}{n}\sum_i (y_i - ah_i -b)\frac{\partial}{\partial a} (y_i - ah_i -b) \\ &= \frac{2}{n}\sum_i (y_i - ah_i -b)h_i \\ &= \frac{2}{n}\sum_i y_ih_i - ah_i^2 -bh_i = 0 \\ &\implies \\ \frac{2}{n}\sum_i y_ih_i -bh_i &= \frac{2}{n}\sum_i ah_i^2 \\ &\implies \\ a\star &= \frac{2}{n}\sum_i \frac{y_ih_i bh_i}{h_i^2} = \frac{2}{n}\sum_i \frac{y_i -b}{h_i} \\ \end{align*}\]Observação 1: se tivéssemos o segundo parâmetro $b$ livre, poderíamos buscá-lo da mesma forma:
\[b\star = \frac{1}{2n}\sum_i y_i - ah_i\]Observação 2: já que o mse não tem uma interpretação humana direta de qualquer jeito (igual ao mae), uma conveniência matemática é normalmente adotada onde ela é definida dividida por $2$:
Isso simplifica as derivadas:
\[\begin{align*} a\star &= \frac{1}{n}\sum_i \frac{y_i -b}{h_i} \\ b\star &= \frac{1}{n}\sum_i y_i - ah_i \end{align*}\]a1 = ((x.shoe_size - b0) / x.height).mean()
mse1 = mse_loss(x.shoe_size, f(x.height, a1, b0))
print(f'MSE = {mse1:.3f}')
plt.figure(figsize=(5, 3))
sns.lineplot(x=As, y=mses)
point_on_curve(mse1, a1, b0)
MSE = 1.930
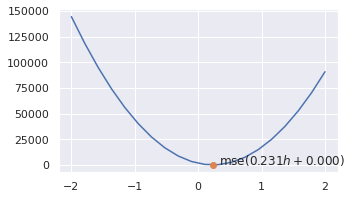
A reta $(a_1, 0)$ pode agora ser utilizada para estimar novas amostras com tamanho de sapato desconhecido, contando que a informação de altura esteja disponível:
sns.scatterplot(data=x, x='height', y='shoe_size', hue='sex', label='real data')
h = 150 + np.arange(80)
p = f(h, a1, b0)
sns.lineplot(x=h, y=p, label=f'f={a1:.3f}x + {b0:.3f}')
plt.tight_layout();
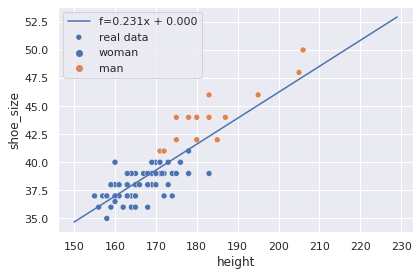
O que acontece quando otimizamos os dois parâmetros atualizados? Podemos atingir um resultado melhor?
b1 = (x.shoe_size - a1*x.height).mean()
mse2 = mse_loss(x.shoe_size, f(x.height, a1, b1))
print(f'MSE updated from {mse1:.3f} to {mse2:.3f} by optimizing parameter b.')
plt.figure(figsize=(5, 3))
sns.lineplot(x=As, y=mses)
point_on_curve(mse2, a1, b1)
MSE updated from 1.930 to 1.930 by optimizing parameter b.
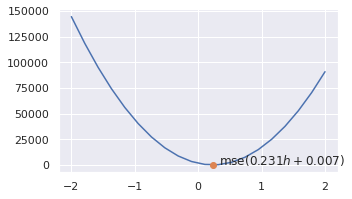
Esse processo de treinamento é interessante por ser eficiente, mas exige que os as variáveis de entrada sejam diferentes de $0$. Quando múltiplas características são apresentadas, essa exigência se generaliza em esperar que a matriz seja inversível.
Solução iterativa da equação
Uma outra forma de definir o treinamento é como um processo de otimização iterativo, onde todos os parâmetros são sujeitos a uma regra de atualização amortecida por um coeficiente (learning rate) por um número limitado de passos (epochs).
Regressões lineares eficientes utilizando o Scikit-learn
from sklearn import metrics
from sklearn.linear_model import LinearRegression
FEATURES = ['height']
model = LinearRegression().fit(x[FEATURES], x.shoe_size)
predicted = model.predict(x[FEATURES])
evaluate(x.shoe_size, predicted)
MSE = 1.901
MAE = 1.074
R² = 0.742
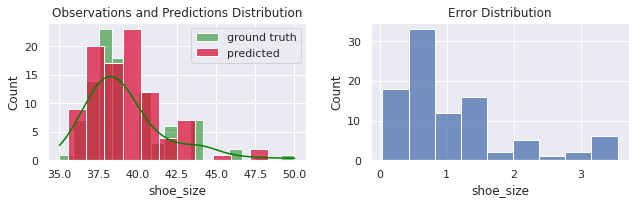
Após otimizar os parâmetros $a$ e $b$, nosso erro caiu muito. Eles estão agora majoritariamente concentrados no intervalo $(0, 1.5)$. Os parâmetros do modelo treinado no scikit-learn tb podem ser diretamente acessados:
model.coef_, model.intercept_
(array([0.24963078]), -3.133275090526716)
Os coeficientes angulares são representados como um vetor pois o scikit considera múltiplas características estão sendo entregues (embora no nosso caso tenha sido uma lista com uma única).
sns.scatterplot(data=x, x='height', y='shoe_size',
hue='sex',
label='real data')
h = 150 + np.arange(80)
a = float(model.coef_)
b = float(model.intercept_)
p = f(h, a, b)
sns.lineplot(x=h, y=p, label=f'f={a:.3f}h + {b:.3f}');
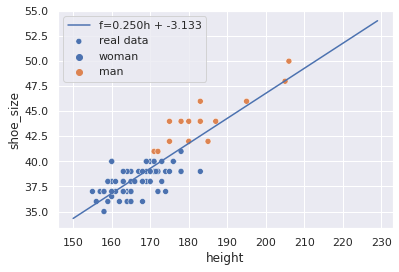
Enriquecendo a informação do dataset
Podemos enriquecer o estimador ao adicionar mais características. Isso aumenta o número de coeficientes utilizados, a granularidade da decisão e, possívelmente, o torna mais acurado:
import traceback
try:
model = LinearRegression().fit(x[['height', 'sex']], x.shoe_size)
except ValueError as e:
traceback.print_exc()
ValueError: could not convert string to float: 'woman'
Por ser um modelo geométrico, ele espera que as features pertençam ao conjunto real. Uma forma de lidar com isso é codificando os rótulos em inteiros:
x['sex_encoded'] = (x.sex == 'woman').astype(int)
x.head()
| sex | height | shoe_size | sex_encoded | |
|---|---|---|---|---|
| 0 | woman | 160.0 | 40.0 | 1 |
| 1 | woman | 171.0 | 39.0 | 1 |
| 2 | woman | 174.0 | 39.0 | 1 |
| 3 | woman | 176.0 | 40.0 | 1 |
| 4 | man | 195.0 | 46.0 | 0 |
Porque a variável sexo é binária neste conjunto (woman e man), ela codifica nos valores 0 e 1. Isso é preprocessamento suficiente para o nosso modelo. Nós estamos usando aqui o que os estatísticos chamam de suposição de efeito fixo: a variável categória exerce uma influencia fixa (constante) sobre a variável observada.
Em outras palavras, estamos criando um modelo que estima o tamanho de sapatos de homens e então adiciona um fator (aprendido) fixo sobre a resposta para estimar o sapatos das mulheres.
Um jeito mais fácil de codificar labels e mantê-las consistentes ao longo de múltiplas execuções é utilizando um label encoder. Neste caso, ele performa exatamente como o nosso código acima:
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
x['sex_encoded'] = le.fit_transform(x.sex)
# joblib.dump(e, '/path/le.p')
# e.transform(...) # then during test, production inference...
x.head()
| sex | height | shoe_size | sex_encoded | |
|---|---|---|---|---|
| 0 | woman | 160.0 | 40.0 | 1 |
| 1 | woman | 171.0 | 39.0 | 1 |
| 2 | woman | 174.0 | 39.0 | 1 |
| 3 | woman | 176.0 | 40.0 | 1 |
| 4 | man | 195.0 | 46.0 | 0 |
Retreinando e avaliando:
FEATURES = ['height', 'sex_encoded']
model = LinearRegression().fit(x[FEATURES].values, x.shoe_size.values)
predicted = model.predict(x[FEATURES].values)
evaluate(x.shoe_size, predicted)
MSE = 1.16
MAE = 0.846
R² = 0.842
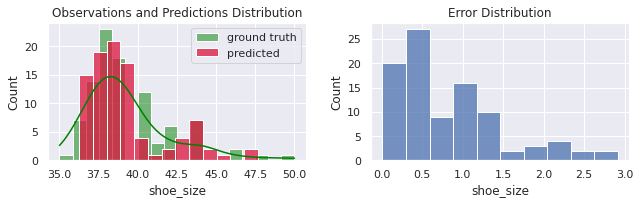
Então não só reduzimos o erro absoluto médio de $1.07$ para $0.85$ (melhora de $21\%$), como também estamos produzindo ainda menos erros grandes (nenhuma amostra teve um erro maior que $3$).
Como ficaram os coeficientes?
model.coef_.round(3), model.intercept_.round(3)
(array([ 0.165, -2.981]), 13.627)
sns.scatterplot(data=x, x='height', y='shoe_size',
hue='sex',
label='real data')
a, b = model.coef_.round(1)
c = model.intercept_.round(1)
h = 150 + np.arange(80).reshape(-1, 1)
s = np.ones(80).reshape(-1, 1)
p_w = model.predict(np.hstack((h, s)))
sns.lineplot(x=h.flatten(), y=p_w, label=f'f={a}h +{b}*1 +{c} (wo)')
s = np.zeros(80).reshape(-1, 1)
p_m = model.predict(np.hstack((h, s)))
sns.lineplot(x=h.flatten(), y=p_m, label=f'f={a}h +{b}*0 +{c} (men)');
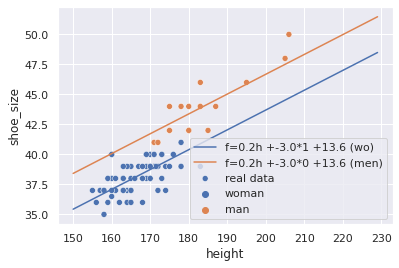
model.predict([[155, 1],
[166, 0]])
array([36.26244771, 41.06102429])
Pela nossa análise no começo, os homens possuiam naturalmente tamanhos de sapato maiores que mulheres. Com o efeito fixo em ação, conseguimos construir “duas” linhas, onde cada linha otimiza o MSE de seu próprio grupo. Efeitos fixos não resolvem todos os problemas. Não vai dar certo quando os diferentes grupos tem âng. de crescimento diferentes, já que esse modelo sempre gera retas paralelas. Nós podemos resolver esses casos com não-lineridade.
Codificando características categóricas não-binárias
Caso mais classes estivessem disponíveis (woman, man, non_binary, unknown, do_not_wish_to_disclosure), elas seriam codificadas nos números inteiros 1, 2, 3, 4e 5:
LabelEncoder().fit_transform(['woman', 'man', 'unknown'])
array([2, 0, 1])
Isso pode provocar um efeito indesejado, já que as classes agora não possuem efeitos fixos distintos, mas compartilharão um único coeficiente que é escalado pelo inteiro codificado.
A forma mais comum de codificar variáveis não binárias é através do one-hot encoding. Neste formato, uma característica categorica com $C$ valores distintos é convertida em $C$ características binárias:
from sklearn.preprocessing import OneHotEncoder
(OneHotEncoder()
.fit_transform([['woman'],
['man'],
['man'],
['do_not_wish_to_disclosure'],
['woman']])
.todense()
.tolist())
[[0.0, 0.0, 1.0],
[0.0, 1.0, 0.0],
[0.0, 1.0, 0.0],
[1.0, 0.0, 0.0],
[0.0, 0.0, 1.0]]
A nova feature $c_i$ assume o valor $1$ quando a amostra pertence à categoria $i$ e $0$ caso contrário. O modelo agora terá liberdade para aprender três parâmetros diferentes e aplica-los sobre a predição dependendo da categoria a qual a amostra pertence.
Regressões lineares utilizando o Tensorflow
A regressão linear pode ser vista como um caso específico de rede neural, composta de uma única camada interna e ativação linear. Atualmente, um framework comum utilizado na implementação de redes é o Tensorflow. Ele permite a criação de regressões da seguinte maneira:
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import InputLayer, Dense
model = Sequential([
InputLayer([2]),
Dense(1, activation='linear', name='predictions')
])
model.compile(
optimizer=tf.optimizers.SGD(learning_rate=.01),
loss='mse',
metrics=['mse', 'mae'])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
predictions (Dense) (None, 1) 3
=================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
_________________________________________________________________
tf.keras.utils.plot_model(model, show_shapes=True)
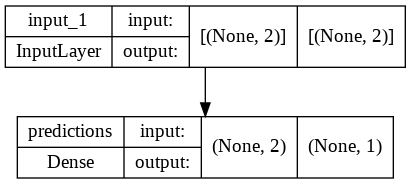
model.fit(x[FEATURES], x.shoe_size, epochs=4);
Epoch 1/4
3/3 [==============================] - 0s 5ms/step - loss: 397999888924672.0000 - mse: 397999888924672.0000 - mae: 11395146.0000
Epoch 2/4
3/3 [==============================] - 0s 5ms/step - loss: 15560207534693492799819011325952.0000 - mse: 15560207534693492799819011325952.0000 - mae: 2253529074892800.0000
Epoch 3/4
3/3 [==============================] - 0s 5ms/step - loss: inf - mse: inf - mae: 437032550431764638597120.0000
Epoch 4/4
3/3 [==============================] - 0s 3ms/step - loss: inf - mse: inf - mae: 83941367757272943147354026934272.0000
Vixe. Infinito definitivamente não parece bom. Redes são modelos paramétricos. Os pesos $w$ são iniciados com valores amostrados de uma distribuição normal, enquanto b com $0$. Ao receber características (ou predizer resultados) muito distantes da normal $(0, 1)$, o modelo precisa percorrer um grande caminho até que seu sinal de saída finalmente escale e translade para a distribuição de saída emparelhado.
O scikit possui a classe StandardScaler, que “aprende” a média e desvio-padrão de um conjunto e consegue “normaliza-lo” removendo a média de cada característica e dividindo pelo desvio padrão.
model = Sequential([
InputLayer([2]),
Dense(1, activation='linear', name='predictions')
])
model.compile(
optimizer=tf.optimizers.SGD(learning_rate=.005),
loss='mse',
metrics=['mse', 'mae'])
from sklearn.preprocessing import StandardScaler
x_scaler, y_scaler = StandardScaler(), StandardScaler()
z = x_scaler.fit_transform(x[FEATURES].values)
y = y_scaler.fit_transform(x.shoe_size.values.reshape(-1, 1))
model.fit(
z, y,
epochs=300,
batch_size=32,
verbose=0,
callbacks=[
tf.keras.callbacks.EarlyStopping('mae',
patience=10,
restore_best_weights=True)
]);
h = pd.DataFrame(model.history.history)
h['epoch'] = h.index
sns.lineplot(
x='epoch',
y='value',
hue='variable',
data=h.melt(['epoch'], ['mse', 'mae'])
);
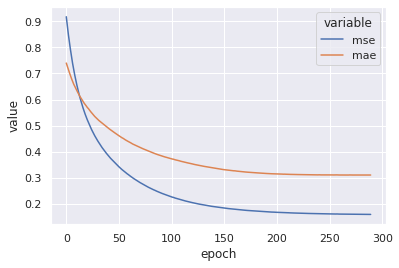
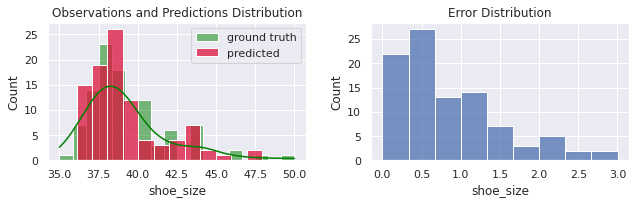
predicted = model.predict(z)
predicted = y_scaler.inverse_transform(predicted).flatten()
evaluate(x.shoe_size, predicted)
MSE = 1.175
MAE = 0.842
R² = 0.84
Próximos passos: features não lineares, redes não-lineares
Não temos mais features para adicionar. Ainda é possível melhorar esse modelo?
Até agora, estamos considerando a relação linear entre as variáveis e o tamanho do sapato. O que aconteceria se esse relacionamento fosse não-linear?
Uma forma de modelar isso é utilizando o transformador PolynomialFeatures, onde as características são utilizadas para a construção dos multiplos termos de um polinômio de grau degree.
Cada termo constitui uma nova característica alimentada ao modelo linear.
Temos então um modelo polinomial (em relação ao dado de entrada) com treinamento
linear.
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
model = make_pipeline(
StandardScaler(),
PolynomialFeatures(degree=2),
LinearRegression()
)
model.fit(x[FEATURES], x.shoe_size)
predicted = model.predict(x[FEATURES])
evaluate(x.shoe_size, predicted)
MSE = 1.092
MAE = 0.823
R² = 0.852
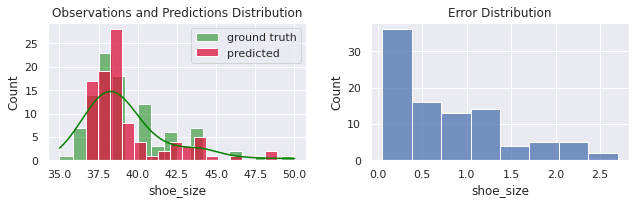
names = [n.replace('x0', FEATURES[0])
.replace('x1', FEATURES[1])
for n in model.named_steps['polynomialfeatures'].get_feature_names_out()]
importance = np.abs(model.named_steps['linearregression'].coef_)
importance /= importance.sum()
sns.barplot(x=names, y=importance)
plt.xticks(rotation=90);
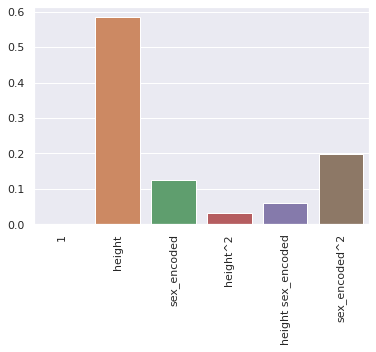
Uma outra forma é não limitar em features polinomiais, mas colocar mais camadas não-lineares na rede, diretamente. Isso dá mais liberdade para o sistema, mas a função de perda (em relação à alguns pesos $\theta$) não é mais uma função linear, o que implica que a equação $\frac{\partial E}{\partial \theta} = 0$ possui múltiplas soluções e nossa busca local nem sempre produz o melhor resultado.
Nós podemos entrar em mais detalhes quando falarmos sobre modelos não-lineares, mas só um exemplo de utilização por enquanto:
from tensorflow.keras.layers import BatchNormalization
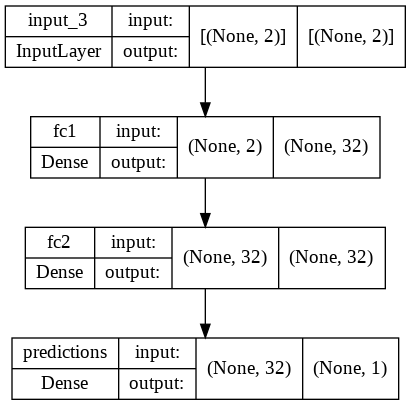
model = Sequential([
InputLayer([2]),
Dense(32, activation='relu', name='fc1'),
Dense(32, activation='relu', name='fc2'),
Dense(1, activation='linear', name='predictions')
])
model.compile(
optimizer='sgd', # or tf.optimizers.SGD(learning_rate=.01),
loss='mse',
metrics=['mse', 'mae'])
tf.keras.utils.plot_model(model, show_shapes=True)
model.fit(
z, y,
epochs=300,
batch_size=32,
verbose=0,
callbacks=[
tf.keras.callbacks.EarlyStopping('mae',
patience=10,
restore_best_weights=True)
]);
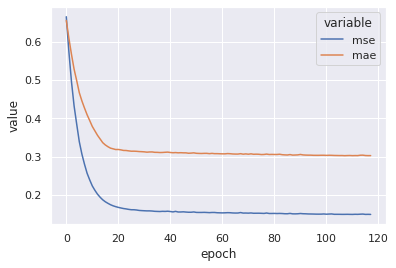
h = pd.DataFrame(model.history.history)
h['epoch'] = h.index
sns.lineplot(
x='epoch',
y='value',
hue='variable',
data=h.melt(['epoch'], ['mse', 'mae']));
predicted = model.predict(z)
predicted = y_scaler.inverse_transform(predicted).flatten()
evaluate(x.shoe_size, predicted)
MSE = 1.096
MAE = 0.82
R² = 0.851
sns.scatterplot(data=x, x='height', y='shoe_size',
hue='sex',
label='real data')
h = 150 + np.arange(80).reshape(-1, 1)
s = np.ones(80).reshape(-1, 1)
s = np.hstack((h, s))
s = x_scaler.transform(s)
s = model.predict(s)
s = y_scaler.inverse_transform(s)
sns.lineplot(x=h.flatten(), y=s.flatten(), label=f'nn wo')
s = np.zeros(80).reshape(-1, 1)
s = np.hstack((h, s))
s = x_scaler.transform(s)
s = model.predict(s)
s = y_scaler.inverse_transform(s)
sns.lineplot(x=h.flatten(), y=s.flatten(), label=f'nn men');
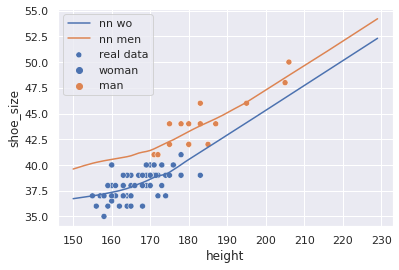
Redes neurais não-lineares com muitas unidades são extremamente flexíveis em seu comportamento, mas são extremamente sensíveis à ruído e irão super-especificar com facilidade. O exemplo acima é só ilustrativo e não deve ser usado pra esse problema.
Generalização e teste
Todas as análises acima foram construídas e avaliadas sobre um único conjunto de dados. Nós modelamos o treinamento como um processo de otimização local e fechado, considerando toda a informação que tinhamos acesso até o momento. Entretando, não é razoável assumir que essas mesmas amostras irão re-indicir durante o estágio de inferência do modelo treinado, já que existem muitos outros compradores utilizando o nosso sistema.
Nós temos uma buraco aqui: nós queremos o modelo que otimiza MAE durante o estágio de inferência, não o que otimiza MAE em treino; mas nós selecionamos os parâmetros de acordo com a segunda métrica. Isso introduz o grande problema de machine learning: overffiting.