Introdução ao aprendizado de máquina, pt. 3

Felizmente, as coisas nem sempre podem ser resolvidas com retas e linearidade. Para resolver esses problemas, vamos falar um pouco sobre não linearidade.

Classificação por regressão logística

Apesar do nome “regressão logíca”, este método remete à uma atividade de classificação. Diferente da regressão, a nossa preocupação do agente inteligente aqui não é estimar um valor, mas sim dar uma resposta: sim ou não.

Como fazer isso sem perdermos o que nós aprendemos acima? Podemos utilizar uma função de ativação. Uma função aplicada sobre a saída de um modelo linear que restringe a resposta à um certo intervalo.

Abaixo estão alguns exemplos de funções de ativação.

• sigmoid (sig), restringindo a saída ao intervalo $[0, 1]$:

  \[\sigma(x) = \frac{1}{1 + e^{-x}}\]

• tangente hiperbólica (tanh), restringindo a saída ao intervalo $[-1, 1]$:

  \[\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

• rectifier linear unit (relu), restringindo a saída ao intervalo $[0, \infty)$:

  \[\text{relu}(x) = \max(x, 0)\]

Veja mais exemplos na página de funções de ativação no Wikipedia.

Usando $\sigma$ (ou função logística), por exemplo, podemos restringir a saída de um modelo de regressão linear à um número entre 0.0 e 1.0, que pode ser interpretado como uma medida de proximidade entre as respostas não e sim:

import numpy as np
from sklearn import datasets

cancer = datasets.load_breast_cancer()

def sigma(x):
  return 1 / (1 + np.exp(-x))

def model(x, w, b, a):
  return a(np.dot(x, w.T) + b)

s, f = cancer.data.shape
w0, b0 = np.random.randn(1, f), np.random.randn(1,)

p = model(cancer.data, w0, b0, sigma)

print('true labels:', cancer.target[:3])
print('predictions:', p[:3])

A função $\sigma$ não é linear. Porém, essa só é aplicada ao sinal após este ser dilatado e deslocado pela operação $x\cdot w + b$. As variáveis de peso $w$ e $b$ se relacionam linearmente com o sinal de entrada $x$. O processo de otimização do sistema é portanto linear com respeito as variáveis treináveis.

Um exemplo prático: Breast Cancer Wisconsin (Diagnostic) Database

Features are computed from a digitized image of a fine needle aspirate (FNA) of a breast mass.

Este conjunto de dados possui 569 amostras descrevendo áreas extraída de tecido de mama através de 30 características, como raio, textura, perímetro e área. As amostras foram então classificadas em 0: malignas e 1: benignas.

from sacred import Experiment
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split

ex = Experiment('training-a-logistic-regression-model')

@ex.config
def my_config():
  workers = 1
  test_size = 1 / 3
  split_random_state = 42

@ex.automain
def main(test_size, workers, split_random_state):
  dataset = load_breast_cancer()
  x_train, x_test, y_train, y_test = train_test_split(
    dataset.data, dataset.target,
    test_size=test_size,
    random_state=split_random_state)

  model = LogisticRegression(n_jobs=workers)
  model.fit(x_train, y_train)

  print('train accuracy:', accuracy_score(y_train, model.predict(x_train)))
  print('test accuracy:', accuracy_score(y_test, model.predict(x_test)))

  print('y:', y_test)
  print('p:', model.predict(x_test))

python training_logistic_regressor with seed=42
train accuracy: 0.955145118734
test accuracy: 0.957894736842
y: [1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 ...]
p: [1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 ...]

Considerações finais em regressão logística

Mesmo com a não-linearidade aplicada sobre o sinal na regressão logística, ela (assim como a regressão linear) ainda é extremamente limitada. Ambas só admitem uma liberdade linear, sempre aproximando uma reposta por uma reta. Para alguns problemas, como Boston ou Breast Cancer, tal liberdade já é suficiente para uma resposta satisfatória. Entretanto, problemas reais muitas vezes são mais difíceis e não-lineares.

Sistemas não-lineares

Uma função de erro $E$, definida sobre um modelo $\sigma(w\cdot x + b)$, não é quadrática e múltiplos pontos de mínimo podems existir:

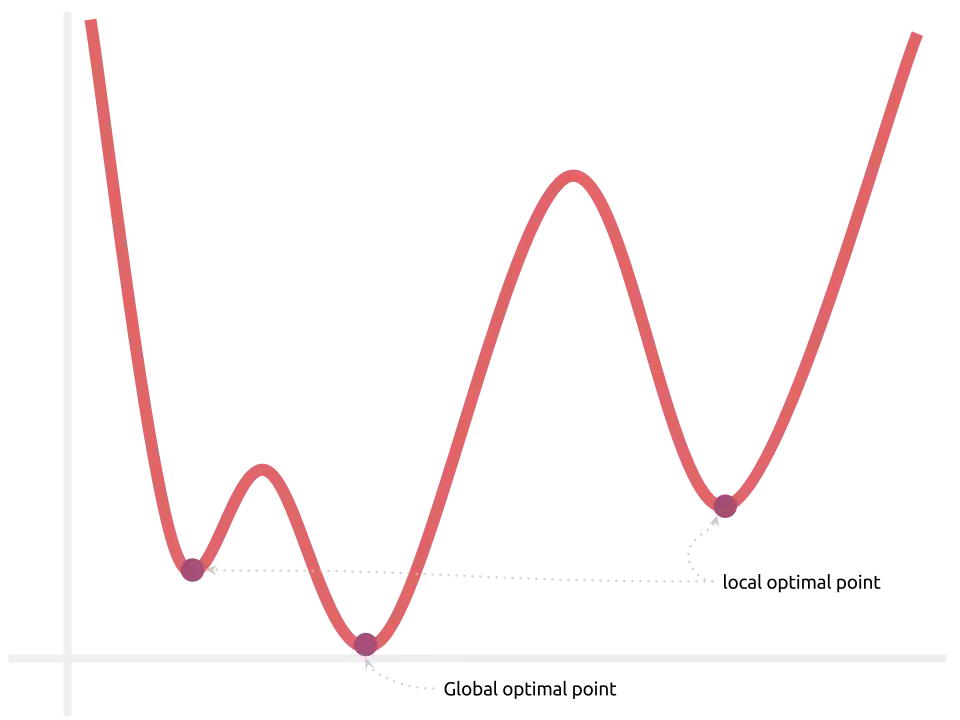
Computar a solução ótima pode ser, portanto, infactível. O ponto positivo é que a função se mantém contínua! Esse é o único requisito para podermos treinar com o método mini-batch stochastic gradient descent. O vetor oposto ao gradiente, computado sobre um ponto-referencial inicial aleatório, ainda aponta para a direção de maior decremento local da função de erro.

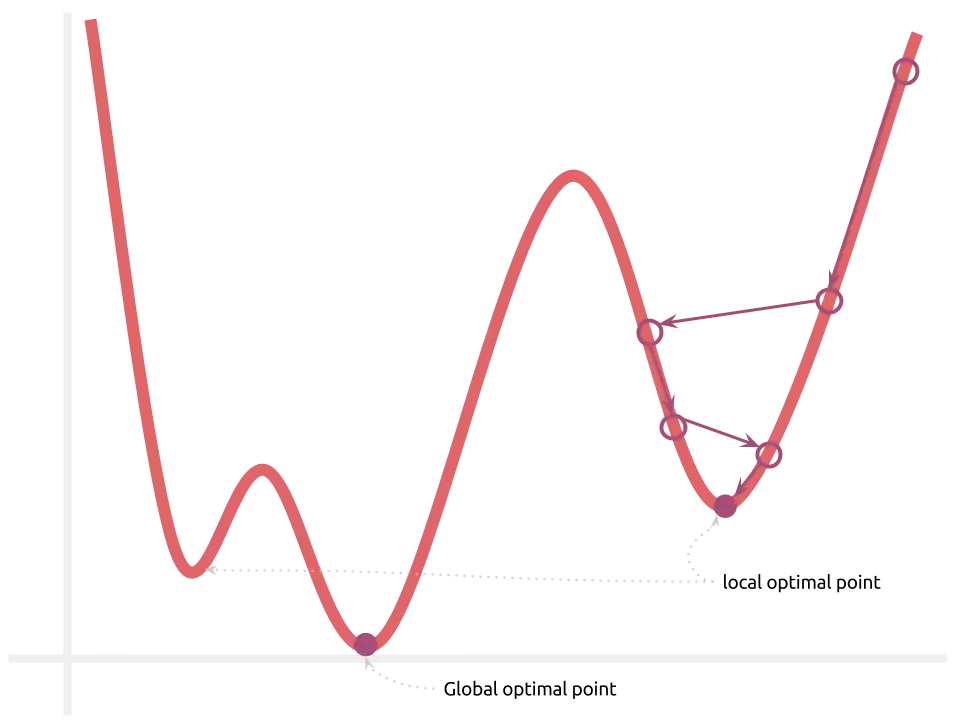
Como o espaço de otimização possui vários pontos de mínimo, a solução não é mais garantidamente ótima. Entretanto, a sensação que temos ao observar os experimentos empíricos conduzidos até hoje é que as soluções encontradas são suficientemente boas, próximas à ótima. É claro que vários melhoramentos ainda podem ser feitos:

• random restart: o treinamento é feito múltiplas vezes, considerando-se múltiplos pontos de início. Os melhores pesos são mantidos.
• simulated annealing: os passos feitos na modificação dos parâmetros do modelo são bruscos e vão graduamente diminuindo. Isso pode ajudar o modelo à superar vales e atingir melhores pontos de mínimo. Este nome remete à ideia de metal sendo modelado nas fornaças, onde ele começa “quente e maleável” e termina “frio e rígido”.

Problemas multi-classes

Nem sempre a resposta é 0 ou 1. Muitas vezes, as amostras no problema em mãos se distribuem por multiplas classes. O conjunto de dados ImageNet, por exemplo, contém imagens de 1000 classes diferentes.

Ainda assim, estes são facilmente traduzidos para o que já sabemos: cada classe pode ser codificada em um número:

x = [...]
y = [0, 0, 4, 1, 2, 3, 1, 1, 1, 0, 0, 3, 1, 0, 0]
classes = np.asarray(['car', 'boat', 'motorcycle', 'airplane', 'spaceshuttle'])
print('decoded labels:', classes[y])

decoded labels: ['car', 'car', 'spaceshuttle', 'boat', 'motorcycle', 'airplane', ...]

E em seguida em um vetor binário, o que comumente chamamos de “one-hot encoding”:

def onehot(y, classes=None):
  if classes is None: classes = len(np.unique(y))
  encoded = np.zeros(len(y), classes)
  encoded[:, y] = 1.0
  return encoded

y = onehot(y)
print(y)

[[1, 0, 0, 0, 0],
 [1, 0, 0, 0, 0],
 [0, 0, 0, 0, 1],
 ...]

Treinamos agora len(classes) regressores logísticos (faça w ser uma matriz, onde cada linha é um regressor diferente). Cada um retornará um valor p_i, contido no intervalo [0, 1], que pode ser interpretado como a probabilidade de uma determinada amostra pertencer à classe i. A classe com maior valor p_i é a mais provável predição da amostra x, e pode ser decodificada pela função argmax:

w0, b0 = r(len(classes), features), r(classes)
onehot_p = model(x, w0, b0, sigma)
decoded_p = np.argmax(p, axis=1)
print('decoded predictions:', classes[decoded_p][:3])

decoded predictions: ['car', 'boat', 'spaceshuttle']

Redes Artificiais

As redes artificiais são modelos de aprendizado de máquina que generalizam regressores lineares, logísticos e SVMs. Na verdade, redes são genéricas o suficiente para aproximar todo e qualquer função (e portanto todo e qualquer modelo).

Muitos autores abordam redes artificiais fazendo um paralelo à redes neurais cerebrais nos seres-humanos, já que a inspiração original era essa. Eu, particularmente, não sou o maior fã dessa visão, pois (a) o conceito de redes neurais não ajuda muito no entendimento da composição formal (o porquê elas funcionam) das redes artificiais e (b) as redes artificias não chegam nem perto de descrever a complexidade do cérebro humano, sendo simplesmente uma aproximação muito distante do modelo teórico que temos atualmente.

Considere o conjunto de dados exemplo abaixo:

Não existe reta que separa as classes vermelho e azul. Dizemos que este conjunto é não linearmente separável. Uma consequência disso é que não existe modelo linear que aprende esse conjunto satisfatóriamente.

Nós precisamos inserir não-linearidade no nosso modelo. Um jeito simples é usar uma função de ativação radial (sim, ela existe). Com essa função, o modelo classificaria todas as amostras que estão dentro de um raio r, transladados por um ponto p (o epicentro do radial), em um grupo e os demais em outro. Isso funciona pra esse caso, mas e se o conjunto fosse um 1-torus (uma rosquinha), 2-torus?

Existem infinitos casos onde a radial não funcionaria, exatamente como existem infintos casos para a linear ou qualquer outra função.

Seria bem da hora se:

• conseguissemos inserir não-linearidade no modelo
• fosse genérico o suficiente para funcionar pra qualquer conjunto, em qualquer forma
• construir isso só com o que nós aprendemos até aqui (w*x + b, sigma(x) etc)

Sim. Isso é possível e é bem simples. Tente pensar um pouco antes de continuar lendo.

Projeção para espaços de maior dimensionalidade

Com duas dimensões, o conjunto é não-linearmente separável; porém ele o seria facilmente com três dimensões:

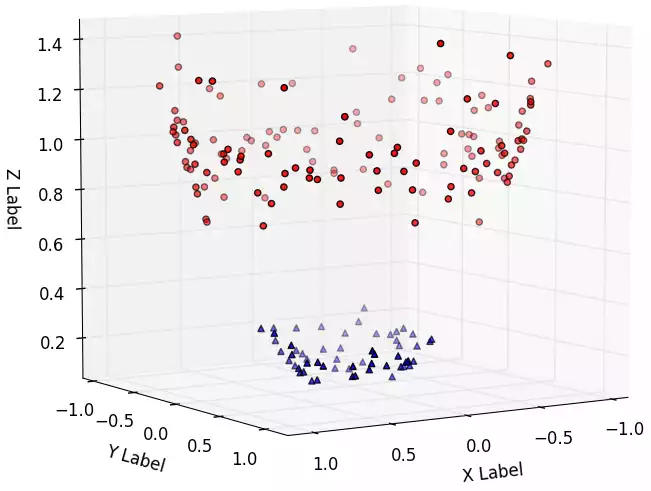
Perceba que é o mesmo conjunto, mas ele foi “projetado” para três dimensões de tal forma que, agora, um hiperplano de decisão é fácilmente desenhável.

Da mesma forma que o nosso regressor logístico aprendeu como discriminar amostras corretamente, podemos treinar um modelo (w, b) (uma camada, na verdade) que aprenda uma projeção não-linear para um espaço de maior dimensionalidade que separe corretamente os dados:

from sklearn import datasets

def dense(x, w, b, name):
  # Apply a 'Dense' layer.
  return np.dot(x, w.T) + b

r = np.random.randn
cancer = datasets.load_breast_cancer()
samples, features = cancer.shape

units = 3

weights = [
  (r(units, features), r(units)),
  (r(1, units), r(1))
]

p = cancer.data
p = dense(p, weights[0][0], weights[0][1], 'fc1')
p = sigma(p)
p = dense(p, weights[1][0], weights[1][1], 'predictions')
p = sigma(p)

O que aconteceu acima:

1. os dados, no espaço de entrada R^2 foram projetados para um um espaço de units (três) dimensões
2. as amostras foram classificadas com base em suas projeções

O termo “units” vem da ideia de que existem “unidades de ativação” em uma certa camada. Antigamente, esse conceito era constantemente denominado de “neurônios”.

Treinando redes de múltiplas camadas

Considere a rede de múltiplas camadas abaixo.

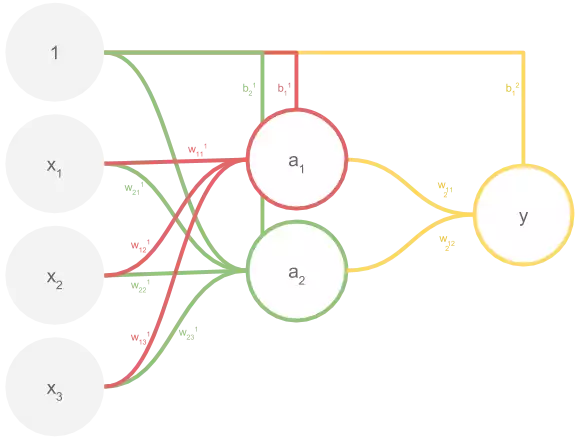
Toda rede pode ser expressa como uma função de uma entrada e de todos os seus parâmetros. A rede acima não é exceção:

Já sabemos calcular o treinamento dos pesos da camada y (w^2 e b^2), usando o método Mini-batch Stochastic Gradient Descent. Falta treinar os pesos das camadas internas. O algoritmo que faz isso é chamado de backward error propagation ou backprop.

A ideia aqui geral do backprop é iterativamente propagar o erro para as camadas anteriores (neste caso, a) e utilizar o SGD para reduzir os parâmetros daquela camada em específico; repetindo o processo até que todas as camadas tenham sido atualizadas.

Aplicada ao problema do conjunto não linearmente separável, é bem possível que a camada interna aprenda a simular a função radial, já que ela é uma resposta válida para o problema. Se isso te faz questionar “por que não usar a radial logo de cara?”, a diferença é que nós aprendemos a função que separa os dados. Se os dados fossem outros, com outra função separadora, teríamos a aprendido sem problemas! :-)

Uma rede com duas camadas é comumente denominada aproximador universal, devido a sua teorica capacidade de aproximar toda e qualquer função. Embora esta afirmação seja apoiada de um teorema, nada podemos afirmar em relação à complexidade necessária para treiná-la.

Últimas dicas (softmax e cross-entropy)

Se o sinal de saída y é one-hot encoded e as amostras se distribuem mutualmente disjuntas umas das outras (uma amostra pertence à uma única classe), podemos substituir a função sigma por uma melhor, o softmax.

softmax exponencializa todos os sinais de entrada, o que os torna extritamente positivos sem desordená-los (pela propriedade da exponencial, “estritamente crescente”, x > y => e^x > e^y). Isso é importante pois mantém unidades com alto nível de ativação como “importantes”, enquanto unidades de baixo nível de ativação se mantém como “não importantes”. Finalmente, ela normaliza cada saída pelo valor total, o que resulta em uma distribuição probabilistica. Isto é, uma imagem de um cachorro entra numa rede que separa entre cachorros, gatos e cavalos. Com sorte, um vetor próximo à (.95, .02, .03) vai ser a resposta.

Além disso, usualmente empregamos a (binary ou categorical) cross-entropy loss em tarefas de classificação:

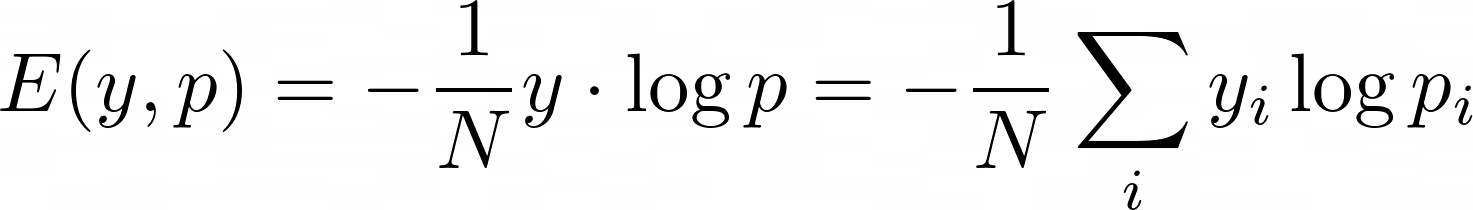
Existem alguns motivos para isso:

• diferente do mse, cross-entropy é uma função limitada superiormente
• a perda é 0 para todas as saídas i onde y_i é 0. Em outras palavras, cross-entropy só se importa em ajustar os pesos da unidade que corresponde à classificação correta da amostra sendo vista, deixando que as outras unidades sejam ajustadas quando amostras correspondentes à elas forem passadas
• mse se constrói em cima da ideia de distância, o que provoca a gradual decrescimento do efeito de atualização dos pesos (ou learning slowdown) durante o treino, quando as saídas reais se aproximam numericamente das saídas esperadas; cross-entropy resolve isso por sua equação não envolver distâncias, explicitamente

Exemplo prático: MNIST

Várias amostras de dígitos escritos a mão. O objetivo aqui é classificar uma amostra entre os 10 diferentes dígitos.

import keras
from keras import callbacks
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import InputLayer, Dense
from sklearn.model_selection import train_test_split

from sacred import Experiment

ex = Experiment('training-dense-network')


@ex.config
def my_config():
    epochs = 20
    batch_size = 128
    num_classes = 10
    valid_size = .25
    early_stopping_patience = 5
    optimizer = 'SGD'
    ckpt = './optimal_weights.hdf5'


@ex.automain
def main(batch_size, num_classes, optimizer, epochs, valid_size, ckpt,
         early_stopping_patience):
    (x_train, y_train), (x_test, y_test) = mnist.load_data()

    x_train = x_train.reshape(60000, 784).astype('float32') / 255
    x_test = x_test.reshape(10000, 784).astype('float32') / 255

    x_train, x_valid, y_train, y_valid = train_test_split(
        x_train, y_train, test_size=valid_size)

    # one-hot encode train and test
    y_train = keras.utils.to_categorical(y_train, num_classes)
    y_valid = keras.utils.to_categorical(y_valid, num_classes)
    y_test = keras.utils.to_categorical(y_test, num_classes)

    model = Sequential([
      InputLayer(shape=[768]),
      Dense(1024, activation='relu', name='fc1'),
      Dense(1024, activation='relu', name='fc2'),
      Dense(num_classes, activation='softmax', name='predictions')
    ])
    model.compile(optimizer=optimizer,
                  loss='categorical_crossentropy',
                  metrics=['accuracy'])

    try:
        model.fit(x_train, y_train,
                  batch_size=batch_size,
                  epochs=epochs,
                  verbose=2,
                  validation_data=(x_valid, y_valid),
                  callbacks=[
                      callbacks.EarlyStopping(patience=early_stopping_patience),
                      callbacks.ModelCheckpoint(ckpt, save_best_only=True, verbose=True)
                  ])
    except KeyboardInterrupt:
        print('interrupted')
    else:
        print('done')

    print('reloading optimal weights...')
    model.load_weights(ckpt)

    score = model.evaluate(x_test, y_test)
    print('test loss:', score[0])
    print('test accuracy:', score[1])

python training_dense_network.py with seed=42
Train on 45000 samples, validate on 15000 samples
Epoch 1/20
44928/45000 [==>.] - ETA: 0s - loss: 1.2223 - acc: 0.7549Epoch 00001: val_loss improved from inf to 0.62518, saving model to ./optimal_weights.hdf5
45000/45000 [====] - 13s 288us/step - loss: 1.2214 - acc: 0.7551 - val_loss: 0.6252 - val_acc: 0.8597
...
Epoch 20/20
44928/45000 [==>.] - ETA: 0s - loss: 0.1678 - acc: 0.9533Epoch 00020: val_loss improved from 0.19170 to 0.18757, saving model to ./optimal_weights.hdf5
45000/45000 [====] - 13s 284us/step - loss: 0.1680 - acc: 0.9532 - val_loss: 0.1876 - val_acc: 0.9470
reloading optimal weights...
test loss: 0.171604911404
test accuracy: 0.9512
INFO - training-a-keras-model - Completed after 0:04:27

Pra ilustrar, podemos exibir alguns dígitos e pedir para o modelo predizer quais são estes. Também pode ser útil visualizar as amostras que estamos errando.

import matplotlib.pyplot as plt

def plot_digits_and_predictions(x, y, p, name):
    plt.figure(figsize=(8, 24))

    for i, (_x, _y, _p) in enumerate(zip(x, y, p)):
        plt.subplot(len(x), 2, 2 * i + 1)
        plt.imshow(_x.reshape(28, 28))
        plt.axis('off')
        plt.title('Digit %i' % int(_y))
        plt.subplot(len(x), 2, 2 * i + 2)
        plt.bar(range(10), _p, color='crimson')
        plt.xticks(range(10), map(str, range(10)))
        plt.yticks([i / 100 for i in range(0, 101, 25)],
                   ['%i%%' % i for i in range(0, 101, 25)])
        plt.title('Label Probability')
    plt.tight_layout()
    plt.savefig(name)

p_test = model.predict(x_test)

plot_digits_and_predictions(x_test[:10],
                            y_test[:10],
                            p_test[:10],
                            'digit-predictions.webp')

misses = np.argmax(p_test, axis=1) != y_test
# retain only the first 10 incorrect predictions
plot_digits_and_predictions(x_test[misses][:10],
                            y_test[misses][:10],
                            p_test[misses][:10],
                            'digit-wrong-predictions.webp')

Pelas imagens na coluna à esquerda abaixo, o modelo parece classificar com bastante certeza as primeiras 10 amostras do conjunto de teste. Quanto à amostras classificadas incorretamente (coluna à direita), observamos que algumas amostras apresentam forte variação no estilo de escrita (o primeiro dígito, por exemplo, não se parece um perfeitamente claro 5).

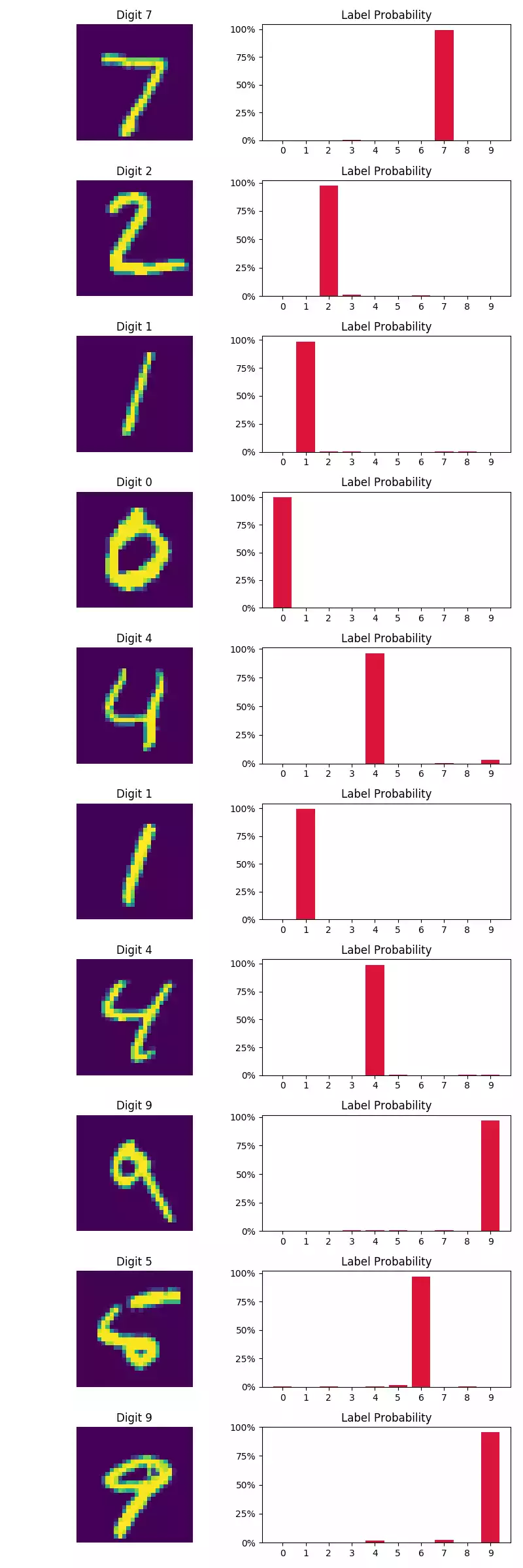
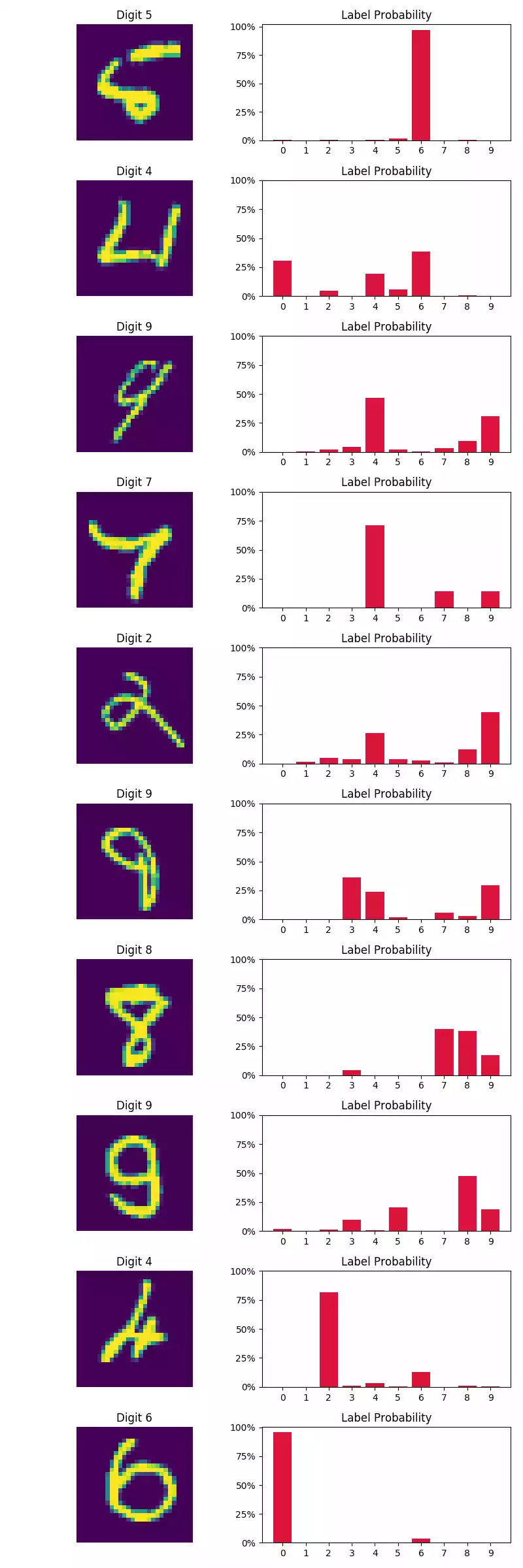
Dica I: tente mudar o otimizador de SGD para adam e veja o grande aumento em performance:

python training_dense_network.py with optimizer="adam" seed=42
Train on 45000 samples, validate on 15000 samples
Epoch 1/20
44800/45000 [==>.] - ETA: 0s - loss: 0.2195 - acc: 0.9344Epoch 00000: val_loss improved from inf to 0.10569, saving model to ./optimal_weights.hdf5
45000/45000 [====] - 18s - loss: 0.2190 - acc: 0.9345 - val_loss: 0.1057 - val_acc: 0.9691
...
Epoch 5/20
44800/45000 [==>.] - ETA: 0s - loss: 0.0277 - acc: 0.9909Epoch 00004: val_loss improved from 0.09160 to 0.07897, saving model to ./optimal_weights.hdf5
45000/45000 [====] - 19s - loss: 0.0279 - acc: 0.9909 - val_loss: 0.0790 - val_acc: 0.9787
Epoch 6/20
44800/45000 [==>.] - ETA: 0s - loss: 0.0200 - acc: 0.9932Epoch 00005: val_loss did not improve
45000/45000 [====] - 16s - loss: 0.0201 - acc: 0.9932 - val_loss: 0.0941 - val_acc: 0.9769
...
Epoch 11/20
44800/45000 [==>.] - ETA: 0s - loss: 0.0138 - acc: 0.9956Epoch 00010: val_loss did not improve
45000/45000 [====] - 16s - loss: 0.0137 - acc: 0.9956 - val_loss: 0.1139 - val_acc: 0.9745
reloading optimal weights...
test loss: 0.107181316118
test accuracy: 0.9765
INFO - training-a-keras-model - Completed after 0:03:12

Acurácia em teste aumentou em metade do número de épocas. Se você está começando e não tem nenhuma informação sobre o problema, vá com adam. Se as coisas não funcionarem como deveriam, tente reduzir o lr ou usar métodos mais simples como o SGD ou Momentum.

Uma rede densa sofre de vários problemas que a torna pouco indicada para para processamento de raw data (imagens, vídeos, audio). Ainda sim, tivemos um bom resultado sobre digits. A verdade é que esse conjunto é um brinquedo. Ele foi pre-processado ao ponto de remover quase todos os problemas comumente encontrados em problemas reais, o que o simplificou à um ponto extremo.

No próximo post, nós vamos ver alguns problemas mais complicados e como redes neurais (profundas) podem ser utilizadas para resolvê-los.