Introdução ao aprendizado de máquina, pt. 2

Modelos lineares e otimização numérica. — October 26, 2017

ML Regression Scikit-Learn Portuguese

Um guia introdutório em Português e Python. Aqui, vamos falar um pouco sobre modelos lineares e seus funcionamentos básicos. Exemplos são dados por trechos de código na linguagem python.

Modelos lineares

Vamos começar pequeno, com uma única dimensão: suponha que você queira estimar números $y := (y_0, y_1, …, y_n)$ (e.g. uma pontuação, um erro, uma quantidade) a partir de outros $x := (x_0, x_1, …, x_n)$, mas não sabe exatamente como essas duas medidas se relacionam.

from sklearn import datasets

samples, features = 1000, 1

# build a dataset with 1000 pairs (x', y') of numbers, with a little noise
x, y = datasets.make_regression(n_samples=samples, n_features=features,
                                n_informative=1, noise=1, random_state=42)
y = y.reshape(1000, 1)

O mais simples dos jeitos é um modelo linear. Ou seja, estimá-lo usando uma reta:

\[p = w\cdot x + b\] 
import numpy as np

# start with random parameters (e.g.: w0 = .024; b = -0.2445)
w0, b0 = np.random.randn(1, features), np.random.randn(1)

def model(x, w, b):
  return x.dot(w.T) + b

p0 = model(x, w0, b0)
print('correct values:', y[:3].flatten())
print('random estimations:', p0[:3].flatten())

correct values: [-29.78727937  15.90389802  -9.14293022]
random estimations: [ 1.18352758  0.76425245  0.99254442]

$w$ e $b$ são parâmetros, variáveis que afetam o comportamento de $p$. Ao alterarmos $w$ e $b$, podemos fazer com que $p$ se torne mais próximo ou mais distante da variável $y$. Pra isso, precisamos primeiro definir uma medida – comumente denominada loss – que indique o quão distante um modelo $p$ está da observação impírica $y$. Uma loss comum é o mean squared error ou MSE:

\[E(y, p) = \frac{1}{2N} (p - y)^2 = \frac{1}{2N} \sum_i (p_i - y_i)^2\] 
def mse(y, p):
  return ((p - y) ** 2).mean()

loss = mse
print('initial loss:', loss(y, p0))

initial loss: 274.493855595

Treinamento

Solução ótima

Minimizar $E(y, p)$ significa aproximar os valores que saem do nosso modelo linear ao valor real, mas como fazer isso? $p$ é linear. Logo, $E$ é uma função quadrática positiva. O que significa que ela tem essa cara, para qualquer um dos parâmetros envolvidos:

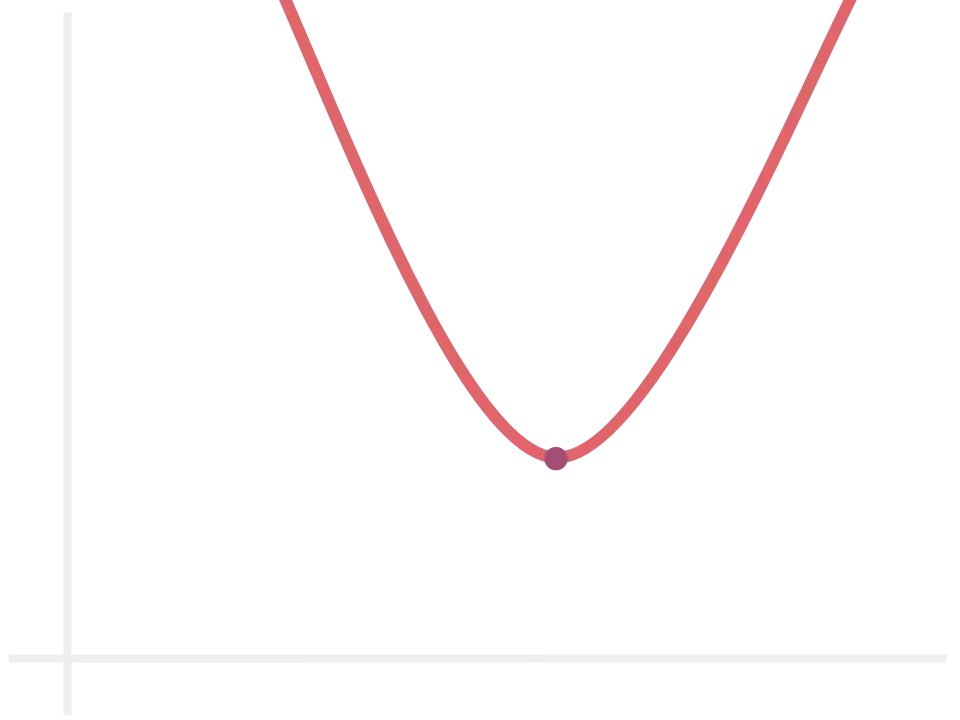
Gráfico de uma função quadrática.

Como podemos observar no gráfico acima, existe um único ponto crítico de mínimo. Usando cálculo I, podemos calcular $w$ e $b$ que levam ao erro mínimo:

Parâmetros ótimos 
def compute_optimal(w, b, x, y):
  w_star = ((y - b) / x).mean(axis=0, keepdims=True)
  b_star = (y - w * x).mean(axis=0)
  return w_star, b_star

w_star, b_star = compute_optimal(w0, b0, x, y)

p_star = model(x, w_star, b_star)
print('best loss:', loss(y, p_star))

best loss: 1.10390441361

Soluções iterativas

Muitas vezes, computar a solução ótima é impossível ou computacionalmente infactível:

  • x possui elementos próximos ao zero
  • o conjunto de dados é muito grande para caber na memória
  • a operação $w\cdot x + b$ é muito demorada devido à grandeza das variáveis
  • a função de erro possui mais de um mínimo (veremos este caso quando passarmos sobre modelos não-lineares)

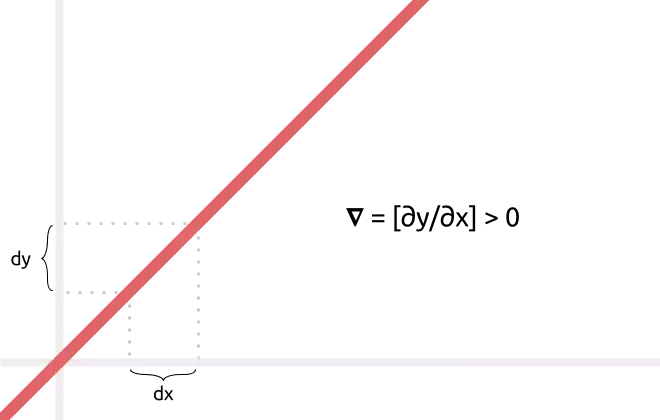
Uma solução possível é executar o treinamento de forma iterativa, utilizando o método chamado Gradient Descent. O gradiente de uma função f é o vetor contendo todas as diferenciais de f e, por definição, aponta na direção de maior aumento da função. Na imagem abaixo, por exemplo: por ser uma reta e por sua inclinação, podemos inferir que o gradiente é um vetor composto por um único elemento e esse é estritamente positivo. Em outras palavras, ele aponta para a direita (o lado positivo do gráfico).

Gradiente de uma função linear.

Online Stochastic Gradient Descent

Aqui, apresentamos cada amostra ao modelo e, logo em seguida, computamos o gradiente.
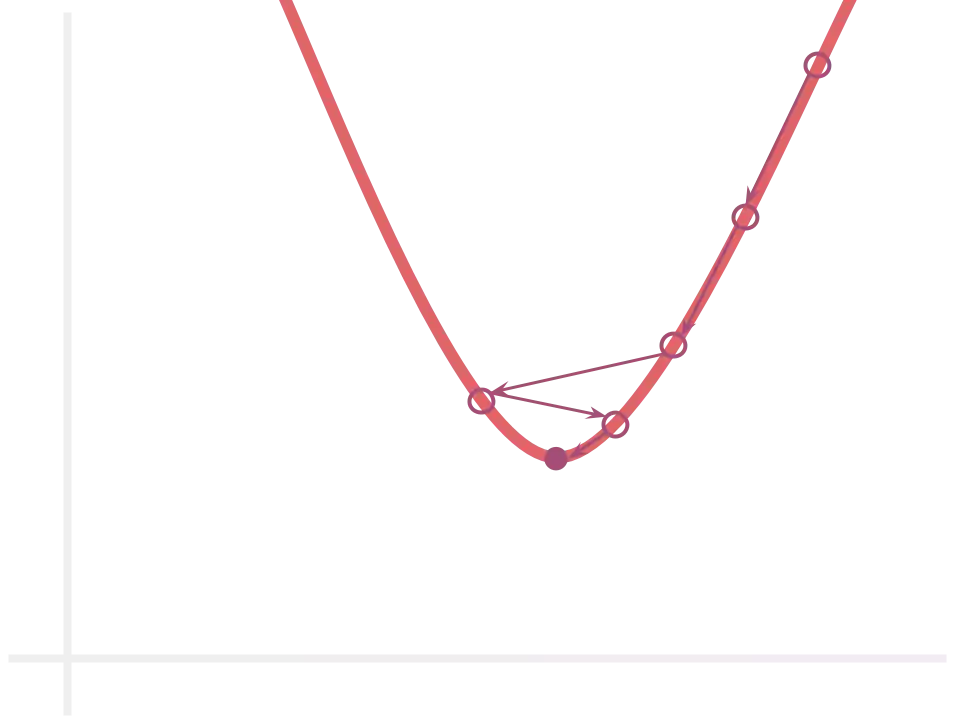
Já que o gradiente aponta para a direção de maior aumento da função $E$, podemos reduzí-la ao somar $w$ e $b$ ao negativo de seus gradientes $-dw$ e $-db$. Desta forma, “caminhamos” para a região de maior decremento da funço $E$. Isto é, a região de menor erro:

Melhoramento iterativo de erro pelo método 'Gradient Descent'.

Usualmente, escalamos a atualização por um fator lr – o learning rate – contido no intervalo $(0, 1]$ a fim de suavizar a modificação aplicada. Isto é importante visto que:

  • somar gradientes de primeira ordem é fundalmentalmente um deslocamento em linha reta em uma função que é uma curva, representando simplesmente uma estimativa
  • o gradiente leva em consideração uma única amostra e não o conjunto como um todo, sendo suscetível a outliers

O processo é repetido por diversas épocas, idealmente até a convergência. Isto é, a estagnação do plano de decisão.

lr = 0.1
epochs = 100
w, b = w0, b0

def compute_gradients(_x, _y, _w, _b):
  if len(_x.shape) == 1:
    # transform a single sample into a list of samples containing a single
    # sample, singularly. A unique sample batch. Just one sample. Simple odd 1.
    _x, _y = (np.expand_dims(e, 0) for e in (_x, _y))
  _p = model(_x, _w, _b)
  de = (_p - _y)
  dw = np.dot(de.T, _x)
  db = de.mean(axis=0)
  return dw, db

def update_gradients(lr, w, b, dw, db):
  w_updated = w - lr * dw
  b_updated = b - lr * db
  return w_updated, b_updated

for epoch in range(epochs):
  for i, (_x, _y) in enumerate(zip(x, y)):
    dw, db = compute_gradients(_x, _y, w, b)
    w, b = update_gradients(lr, w, b, dw, db)

p = model(x, w, b)
print('final loss:', loss(y, p))

final loss: 1.44465388371

Uma característica importante do treinamento online é que ele rapidamente reduz o MSE, já que computar $\text _x$ é muito mais rápido do que $x$. Outra é que ele frequentemente se materializa como um processo divergente, já que o processo de atualização do modelo só enxerga uma única instância e ignora as demais.

Podemos melhorar essa situação com um “meio termo”. A estratégia de batches.

Mini-batch Gradient Descent

No treinamento por batches, um subconjunto de amostras pequeno, porém significativo (que corretamente representa a distribuição dos dados de treinamento) é selecionado. O gradiente é então computado sobre o batch:

from math import ceil

batch_size = 128
batches = ceil(samples / batch_size)
w, b = w0, b0

for epoch in range(epochs):
  for batch in range(batches):
    _x = x[batch * batch_size:(batch + 1) * batch_size]
    _y = y[batch * batch_size:(batch + 1) * batch_size]

    dw, db = compute_gradients(_x, _y, w, b)
    w, b = update_gradients(lr, w, b, dw, db)

A mais simples forma de induzir estabilidade na distribuição do batch é através do que chamamos de stochastic mini-batch gradient descent, onde as amostras são aleatóriamente selecionadas:

def shuffle_samples(x, y):
  # shuffle dataset while maintaining original pairs together
  p = np.arange(len(x))
  np.random.shuffle(p)
  return x[p], y[p]

for epoch in range(epochs):
  x, y = shuffle_samples(x, y)

  for batch in range(batches):
    _x = x[batch * batch_size:(batch + 1) * batch_size]
    _y = y[batch * batch_size:(batch + 1) * batch_size]

    dw, db = compute_gradients(_x, _y, w, b)
    w, b = update_gradients(lr, w, b, dw, db)

Este (ou variações deste) é um dos método mais utilizados no treinamento de redes neurais, atualmente.

Teste

Os passos acima buscam o erro seja mínimo para as amostras de treinamento. Entretanto, nosso objetivo não é criarmos um IF/ELSE gigante, que acerta todas as amostras de treino mas erra terrívelmente para quaisquer amostras futuras.

Queremos que ele seja genérico o suficiente para ser reaplicado em situações futuras, em amostras de teste. Portanto, usualmente subdividimos o conjunto de dados em:

  • treino: conjunto de amostras utilizadas para se atualizar os parâmetros do modelo.
  • teste: conjunto de dados onde o modelo é aplicado e a loss registrada. Como o modelo não viu nenhuma destas amostras durante o treino, podemos supor que é assim que ele se comportará em amostras futuras.

Se existem hiper-parâmetros (lr, batch_size) ou se o treinamento é iterativo, o conjunto de treino é normalmente separado em treino e validação. Assim, modificamos os parâmetros com base nos gradientes computado sobre as amostras de treino, mas mantemos o registro dos parâmetros que resultarem menor erro nas amostras valiação. Isto é, estamos salvando os parâmetros que melhor generalizam o problema.

from sklearn.model_selection import train_test_split

test_size = 1 / 3
valid_size = 1 / 4
best_valid_error = np.inf
w, b = w0, b0

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=test_size)
x_train, x_valid, y_train, y_valid = train_test_split(x_train, y_train, test_size=valid_size)

for epoch in range(epochs):
  x_train, y_train = shuffle_samples(x_train, y_train)

  for batch in range(batches):
    _x = x_train[batch * batch_size:(batch + 1) * batch_size]
    _y = y_train[batch * batch_size:(batch + 1) * batch_size]
    dw, db = compute_gradients(_x, _y, w, b)
    w, b = update_gradients(lr, w, b, dw, db)

  p_valid = model(x_valid, w, b)
  if loss(y_valid, p_valid) <= best_valid_error:
    best_valid_error = loss(y_valid, p_valid)
    w_star, b_star = (w, b)

p_test = model(x_test, w_star, b_star)
print('test mse:', loss(y_test, p_test))

Múltiplas características

Como funcionaria se um valor $y$ estivesse sendo regredido de uma amostra $x$ composta por mais de uma característica? Nenhum segredo aqui. Na verdade, todas as seções acima (com exceção de solução ótima) já lidam perfeitamente com esse caso.

Com múltiplas características, uma amostra se torna um vetor de números e o conjunto $x$ uma matriz. A fim de garantir liberdade ao modelo, definimos $w$ também como um vetor, onde cada elemento é um coeficiente que multiplica um atributo diferente:

x, y = dummy_dataset(samples=1000, features=32)

w, b = np.random.randn((1, 32)), np.random.randn(1)

p = model(x, w, b)
assert p.shape == y.shape

Resumindo:

  • Se $x$ e $w$ são números, há uma única característica e dot é a múltiplicação convencional nos Reais, resultando em um número que pode ser somado à $b$.
  • Se $x$ e $w$ são vetores, dot é o produto interno, resultando em um número que também pode ser somado à $b$.

O gradiente continua funcionando do mesmo jeito, já que mean(axis=0) garante que somente a primeira dimensão (contendo a diferença entre amostras) seja reduzida, preservando a diferença entre os diferentes parâmetros em $w$ (contidos na segunda dimensão).

Nota I: se você está se perguntando “por quê $b$ não virou um vetor (digamos, $c$) também?”, a reposta é simples: ele virou sim, mas se supormos $b = w\cdot c$, então $w\cdot (x+c) = w\cdot x+b$. Com isso, podemos dar um “jeito brasileiro” e simplesmente guardar um número em vez do vetor inteiro. :-)

Nota II: o método apresentado em solução ótima exige dividir a equação por $x_i$. No caso de múltiplas características, isso equivale a inverter a matrix $x$, o que nem sempre possível. :-(

Um exemplo prático de regressão: Boston

Este conjunto de dados contém informações sobre casas na região metropolitana de boston, relacionando atributos gerais ao custo de mercado efetivo destas. Não sabemos exatamente como cada um desses atributos afetam o custo, mas podemos usar um modelo linear para descobrir isso:

from sacred import Experiment

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error as mse
from sklearn.model_selection import train_test_split

ex = Experiment('training-linear-regressor')


@ex.config
def my_config():
  workers = 1
  test_size = 1 / 3
  split_random_state = 42


@ex.automain
def main(test_size, workers, split_random_state):
  dataset = load_boston()
  x_train, x_test, y_train, y_test = train_test_split(
      dataset.data, dataset.target,
      test_size=test_size,
      random_state=split_random_state)

  model = LinearRegression(n_jobs=workers)
  model.fit(x_train, y_train)

  print('train mse:', mse(y_train, model.predict(x_train)))
  print('test mse:', mse(y_test, model.predict(x_test)))

  print('y:', y_test[:5])
  print('p:', model.predict(x_test)[:5])


$ python training_linear_regressor.py with seed=42
train mse: 23.0559695699
test mse: 20.6179622853
y: [ 23.60  32.40  13.60  22.80  16.10 ...]
p: [ 28.55  36.61  15.68  25.51  18.76 ...]

MSE em teste está em 20.6k, o que significa que o modelo aproxima o preço verdadeiro $p$ por uma margem de $(p - 4.54k, p + 4.54k)$. Parece bom o suficiente pra mim. Por enquanto.

Lembre-se que eu os resultados dependem das condições iniciais, que são aleatórias. Precisamos então pensar um pouco em reproducibilidade. O jeito mais fácil, na minha opinião, é usando o módulo sacred, que – entre várias coisas – ajusta automaticamente a semente do gerador pseudo-aleatório para 42 quando executamos o script com os argumentos with seed=42. Dê uma olhada no meu mini post sobre o sacred e na documentação para entender melhor como ele funciona.

Próximo post: não linearidade

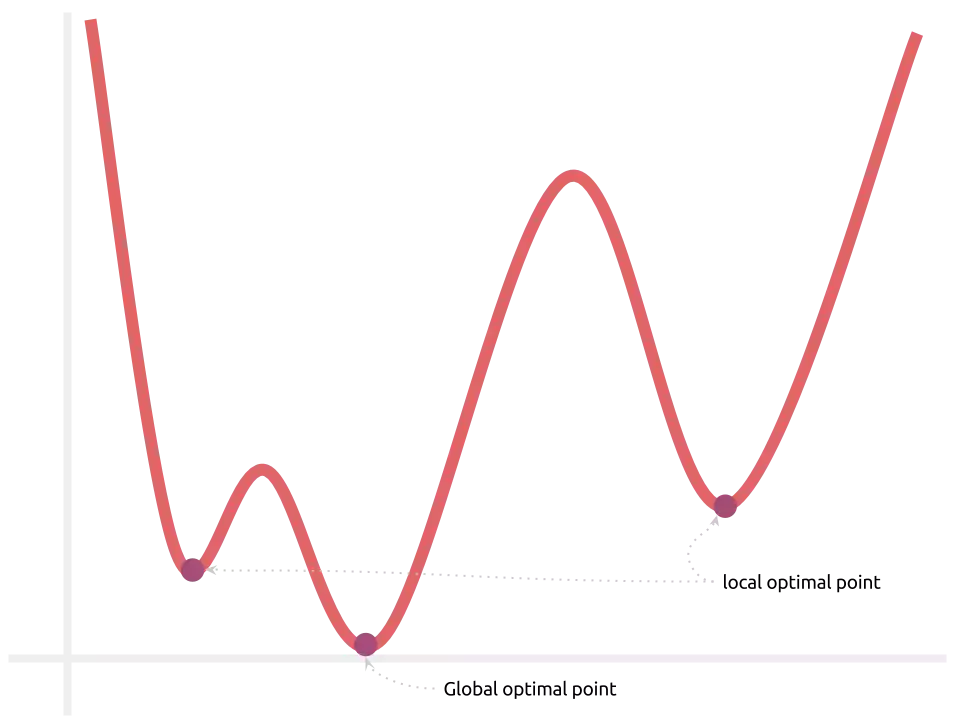
Gráfico de uma função não linear, de ordem superior à quadrática.

Infelizmente, as coisas nem sempre serão resolvidas com retas e linearidade. Resolver esses problemas exigem a utilização de modelos não-lineares, o que envolve várias outras peculiaridades. Só para instigar, pense: o que aconteceria com o erro se nosso modelo de decisão não fosse uma reta? O que acontece com o espaço de otimização se existem multiplas características?