Introdução ao aprendizado de máquina, pt. 4

Na parte 3, eu mostrei alguns modelos não lineares e como eles lidam com a tarefa de classificação. No geral, redes densas possuem duas ou três camadas. Isso acontece pois observa-se empiricamente que o ganho em validation loss não segue linearmente com a adição de mais camadas. Além disso, este pequeno ganho também pode ser alcançado ao simplesmente aumentar o número de unidades nas camadas já presentes na rede densa.

Por quê precisamos da ideia de deep-learning e deep-models, então? Vamos voltar à imagem da introdução:

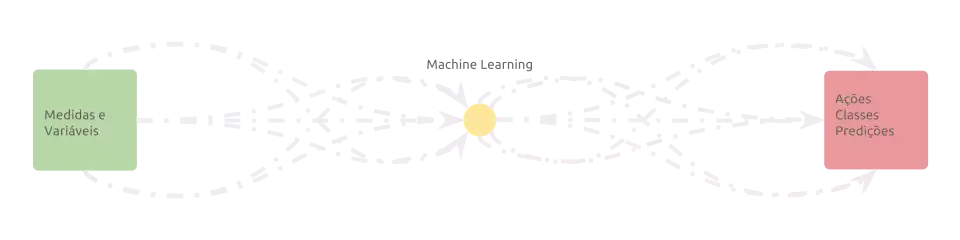
O aprendizado de máquina clássico se focou em preencher a lacuna do centro do fluxo. O “como” resolver um problema. Os modelos clássicos, portanto, funcionam bem para problemas que são difíceis de resolver, mas facilmente descritos de forma numérica.

Entretanto, como resolver problemas que são difíceis de serem descritos computacionalmente? Abaixo estão alguns exemplos de problemas assim:

Direção de carros - isso pode ser decomposto em algumas sub-atividades, como regredir a curvatura da pista, localizar os carros adjacentes e regredir a velocidade ótima.
Classificação de cancer de pele - isso exige uma coleta confiável de informações das regiões de interesse.
Sintetização de texto - a construção de significado sobre tuplas ordenadas de códigos que representem letras, palavras ou sentenças.

Todos os exemplos acima não são fácilmente representados em uma estruturada de dados. Por exemplo, não há forma consistente de se extraír automaticamente informações como diâmetro e forma de pedaços de tecido. Eles podem, entretanto, ser capturados por ferramentas comuns à nós humanos e representados por trechos de dados não estruturados (ou raw data), como fotos, vídeos e trechos de texto e audio.

Um subconjunto de algoritmos – as redes convolucionais, em especial – os quais são comumente referidos como “deep-learning methods” foram criados na tentativa de inferir informações semânticas de dados não estruturados. Eles são integrados ao início do pipeline de processamento e podem, portanto, ser vistos como uma extensão do aprendizado de máquina ‘clássico’:

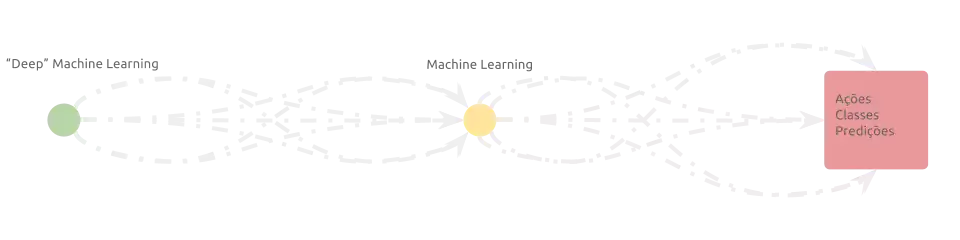
Aprendizado de máquina 'profundo' — Aprendizado de máquina profundo.

Descrição das camadas convolucionais

Vamos entender como as redes convolucionais funcionam na prática. Considere a imagem do urso koala abaixo:

A imagem de um koala sobre uma árvore. — A fotografia de um koala sobre uma árvore.

Primeiramente, confirme que você tem a biblioteca keras instalada com pip install --upgrade keras. Com o código abaixo, podemos carregar o koala em memória, criar um batch de imagens (que nesse caso contém só uma mesmo) e preprocesá-lo:

import numpy as np
from keras.preprocessing.image import load_img, img_to_array

channels = 3
input_shape = (299, 299, channels)

def preprocess_input(x):
  # transform pixel' values in [0, 255] to [-1.0, 1.0] interval.
  return x / 127.5 - 1.

koala = img_to_array(load_img('./koala.webp', target_size=input_shape))
x = np.expand_dims(koala, 0)
x = preprocess_input(x)
print(x.shape)

(1, 299, 299, 3)

Preprocessar os dados de entrada reduz a ordem dos números que representam o problema, trazendo mais estabilidade para o processo seguinte, que envolve dezenas/centanas multiplicações de matrizes.

As redes convolucionais são subconjuntos das redes densas (vistas na parte 3) e lembram vagamente o cortex visual humano, o conceito originalmente utilizado em seu desenvolvimento.

Em uma camada convolucional, uma unidade não se conecta “densamente” em relação à camada de entrada, mas apenas à uma pequena porção local do seu campo de recepção visual. Os parâmetros da unidade promovem uma ativação de alta intensidade na detecção de um determinado padrão:

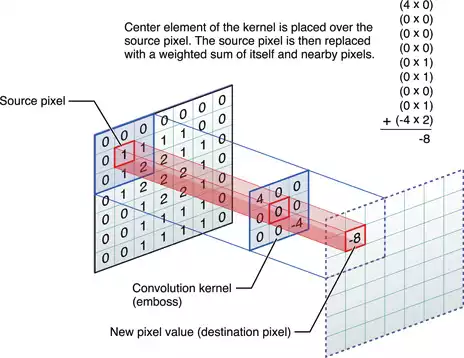
Exemplo de Hadamard entre uma região local de um sinal de entrada e um kernel, seguido de uma soma redutiva. Disponível em: stackexchange.com

Podemos escrever o processamento de uma única região do receptor visual usando python:

local_field = 0, 0
k0_window = [3, 3]
k0_w = np.random.randn(*k0_window, channels)

local_x = x[:, local_field[0]:local_field[0] + k0_window[0],
               local_field[1]:local_field[1] + k0_window[1]]

y = (local_x * k0_w).sum(axis=(1, 2, 3))
print('activation:', y)

activation: [ 0.14476406]

Criar mais unidades com parâmetros similares – mas conexos à outras regiões do campo de recepção visual – promove um comportamento similar distribuido por todas as porções de sua visão. É claro, você pode interpretar essas “múltiplas unidades” como uma “única unidade deslisante” sobre todo o campo de recepção visual. Por outro lado, a construção de unidades de estados físicos distíntos promove uma alta ativação durante a aparição de padrões visuais diferentes:

kernels = 32
k0_window = [3, 3]
k0 = {'w': np.random.randn(kernels, *k0_window, channels), 'b': np.zeros(kernels)}

def conv2d(x, k, stride=1):
  batch_size, height, width, kernels = x.shape
  kernels, k_height, k_width, k_depth = k['w'].shape

  y = np.empty((batch_size, height // stride, width // stride, kernels))

  for l in range(kernels):
    for i in range(0, y.shape[1], stride):
      for j in range(0, y.shape[2], stride):
        # shift i and j so they are in the center of the local receptor field.
        i, j = max(i - k_height // 2, 0), max(j - k_height // 2, 0)
        _x = x[:, i:i + k_height, j:j + k_width, :] * k['w'][l]
        y[:, i, j, l] = _x.sum(axis=(1, 2, 3))

  return y

def add_bias(x, k):
  return x + k['b']

def relu(x):
  return np.maximum(x, 0)

y = conv2d(x, k0, stride=1)
y = add_bias(y, k0)
y = relu(y)
print(y.shape)

(1, 299, 299, 32)

O sinal de entrada, com formato (batch_size, height, width, 3) passa pelas funções e é transformado em um sinal com formato (batch, height, width, kernels), onde cada uma das kernels matrizes representa a indensidade em que um determinado padrão apareceu no sinal de entrada.

O empilhamento das camadas convolucionais promove a composição das ativações, formando padrões estruturados. Porém, aumentar o número de kernels iria requerer grandes quantidades de memória e processamento. A fim de aliviar esse problema, usualmente combinamos as duas abordagens abaixo:

Aumentamos o parâmetro stride em conv2d, o que resulta em uma convolução espaçada por saltos mais largos:

y = conv2d(x, k0, stride=2)
y = add_bias(y, k0)
y = relu(y)
print(y.shape)

(1, 149, 149, 32)

Executamos intercaladamente uma função denominada pooling, que tem como objetivo trocar precisão (em relação ao local do campo receptor visual ativado) pela redução do requisito de memória para se armazenar aquele sinal.
Duas formas de poolings são extremamente utilizados:
- max-pooling 2D: somente a maior ativação em uma janela definida é retida. O resto do sinal é descartado.
- avg-pooling 2D: a média de ativações em uma janela definida é retida.

Descrição das camadas de pooling

def _pooling2d(x, f, window=(2, 2)):
  batch_size, height, width, kernels = x.shape
  y = np.empty((batch_size, height // window[0], width // window[1], kernels))

  for b in range(batch_size):
      for i in range(0, height, window[0]):
        for j in range(0, width, window[1]):
          y[b, i, j] = f(x[b, i:i + window[0], j:j + window[1]])

  return y

def max_pooling2d(x, window=(2, 2)):
  return _pooling2d(x, np.max, window)

def avg_pooling2d(x, window=(2, 2)):
  return _pooling2d(x, np.mean, window)

print('input shape:', y.shape)
y = max_pooling2d(y, window=(2, 2))
print('output shape:', y.shape)

input shape:  (299, 299, 32)
output shape: (149, 149, 32)

Após uma certa quantidade de camadas, observamos unidades repondendo à padrões de alto valor semântico, como faces, objetos ou animais:

layers = [
  {'w': np.random.randn(32, *k0_window, channels), 'b': np.zeros(32)},
  {'w': np.random.randn(32, *k0_window, 32), 'b': np.zeros(32)},
  {'w': np.random.randn(64, *k0_window, 32), 'b': np.zeros(64)},
  {'w': np.random.randn(128, *k0_window, 64), 'b': np.zeros(64)},
]

def conv2d_b_relu(x, k, stride=1):
  x = conv2d(x, k, stride=stride)
  x = add_bias(x, k)
  x = relu(x)
  return x

print('input shape:', y.shape)
y = conv2d_b_relu(y, layers[0], stride=2)
y = conv2d_b_relu(y, layers[1], stride=2)
y = max_pooling2d(y, window=(2, 2))
y = conv2d_b_relu(y, layers[2], stride=2)
y = max_pooling2d(y, window=(2, 2))
y = conv2d_b_relu(y, layers[3], stride=2)
y = max_pooling2d(y, window=(2, 2))
print('output shape:', y.shape)

input shape:  (1, 299, 299, 32)
output shape: (1, 37, 37, 128)

Por fim, alimentamos um modelo clássico (uma rede densa, como exemplo) com a saída desta rede convolucional, criando assim um pipeline completo – porém eficiente – de classificação:

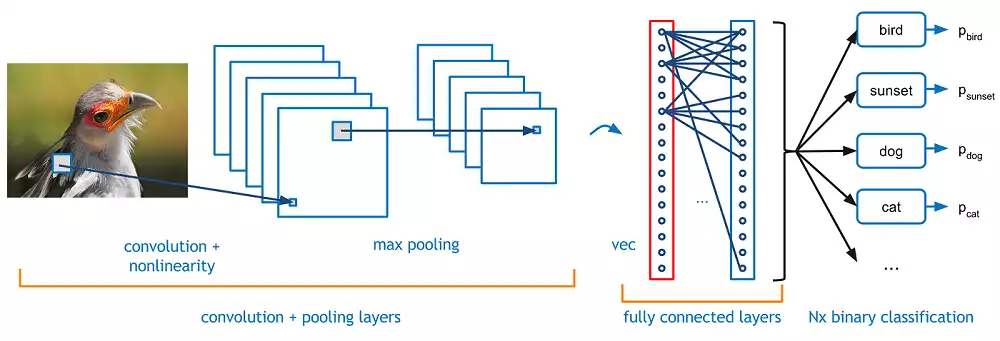
Exemplo de rede convolucional aplicada ao processamento de imagens. Disponível em: adeshpande3.github.io

num_classes = 10

def flatten(x):
  batch_size, height, width, kernels = x.shape
  return x.reshape(batch_size, -1)

layers += [
  {'w': np.random.randn(256, 128), 'b': np.zeros(256)},
  {'w': np.random.randn(num_classes, 256), 'b': np.zeros(num_classes)}
]

y = flatten(y)
y = dense(y, layers[5])
y = relu(y)
y = dense(y, layers[7])
y = softmax(y)

Exemplo de classificação com redes convolucionais

cifar10 é um conjunto composto por imagens RGB (32, 32, 3) pertencentes à 10 classes distintas (avião, automóvel, pássaro etc).

Exemplo de amostras em cifar10. Disponível em: cs.toronto.edu/~kriz/cifar.html

Usando o que foi descrito até agora, podemos criar uma rede que classifica as amostras:

import keras
from keras import Model, Input, callbacks
from keras.datasets import cifar10
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
from sklearn.model_selection import train_test_split

from sacred import Experiment

ex = Experiment('training-conv-network')


@ex.config
def my_config():
    epochs = 20
    batch_size = 128
    num_classes = 10
    valid_size = .25
    early_stopping_patience = 5
    optimizer = 'adam'
    ckpt = './weights.hdf5'


@ex.automain
def main(batch_size, num_classes, optimizer, epochs, valid_size, ckpt,
         early_stopping_patience):
    (x_train, y_train), (x_test, y_test) = cifar10.load_data()

    print('image shapes:', x_train.shape[1:])

    x_train = (x_train - x_train.mean(axis=0)) / x_train.std(axis=0)
    x_test = (x_test - x_test.mean(axis=0)) / x_test.std(axis=0)

    x_train, x_valid, y_train, y_valid = train_test_split(
        x_train, y_train, test_size=valid_size)

    # one-hot encode train and test
    y_train = keras.utils.to_categorical(y_train, num_classes)
    y_valid = keras.utils.to_categorical(y_valid, num_classes)
    y_test = keras.utils.to_categorical(y_test, num_classes)

    x = Input(shape=x_train.shape[1:])
    y = Conv2D(32, kernel_size=(3, 3), activation='relu', name='conv2d_1')(x)
    y = Conv2D(32, kernel_size=(3, 3), activation='relu', name='conv2d_2')(y)
    y = MaxPooling2D(2, name='maxpool_2')(y)
    y = Conv2D(64, kernel_size=5, activation='relu', name='conv2d_3')(y)
    y = Conv2D(64, kernel_size=5, activation='relu', name='conv2d_4')(y)
    y = Flatten()(y)
    y = Dense(1024, activation='relu', name='fc1')(y)
    y = Dense(1024, activation='relu', name='fc2')(y)
    y = Dense(num_classes, activation='softmax', name='predictions')(y)

    model = Model(inputs=x, outputs=y)
    model.compile(optimizer=optimizer,
                  loss='categorical_crossentropy',
                  metrics=['accuracy'])

    try:
        model.fit(x_train, y_train,
                  batch_size=batch_size,
                  epochs=epochs,
                  verbose=2,
                  validation_data=(x_valid, y_valid),
                  callbacks=[
                      callbacks.EarlyStopping(patience=early_stopping_patience),
                      callbacks.ModelCheckpoint(ckpt, save_best_only=True, verbose=True)
                  ])
    except KeyboardInterrupt:
        print('interrupted')
    else:
        print('done')

    print('reloading optimal weights...')
    model.load_weights(ckpt)

    score = model.evaluate(x_test, y_test, verbose=0)
    print('test loss:', score[0])
    print('test accuracy:', score[1])

python training_conv_network.py with seed=42

Epoch 00001: val_loss improved from inf to 1.20643, saving model to ./weights.hdf5
 - 169s - loss: 1.5395 - acc: 0.4352 - val_loss: 1.2064 - val_acc: 0.5673
Epoch 2/20
Epoch 00002: val_loss improved from 1.20643 to 1.05511, saving model to ./weights.hdf5
 - 149s - loss: 1.1084 - acc: 0.6027 - val_loss: 1.0551 - val_acc: 0.6270
Epoch 3/20
Epoch 00003: val_loss improved from 1.05511 to 0.90021, saving model to ./weights.hdf5
 - 151s - loss: 0.8959 - acc: 0.6817 - val_loss: 0.9002 - val_acc: 0.6859
Epoch 4/20
Epoch 00004: val_loss improved from 0.90021 to 0.85776, saving model to ./weights.hdf5
 - 148s - loss: 0.7592 - acc: 0.7307 - val_loss: 0.8578 - val_acc: 0.7046
Epoch 5/20
Epoch 00005: val_loss did not improve
 - 149s - loss: 0.6478 - acc: 0.7695 - val_loss: 0.8755 - val_acc: 0.6972
Epoch 6/20
Epoch 00006: val_loss did not improve
 - 171s - loss: 0.5393 - acc: 0.8092 - val_loss: 0.8609 - val_acc: 0.7235
Epoch 7/20
Epoch 00007: val_loss did not improve
 - 169s - loss: 0.4159 - acc: 0.8494 - val_loss: 0.9289 - val_acc: 0.7171
Epoch 8/20
interrupted
reloading optimal weights...
test loss: 0.8785748579978943
test accuracy: 0.7031
INFO - training-conv-network - Completed after 0:19:55

Perceba que, por não ter acesso a uma placa de vídeo, levou quase 20 minutos para executar um pouco mais que 7 epochs. Neste momento, eu fiquei com preguiça e decidi interromper o treinamento.

Utilizando redes prontas

Muitas plataformas utilizadas em Machine Learning contém modelos, redes e ferramentas prontas. Esse é o caso do Keras. Você pode encontrar diversas arquiteturas já treinadas no módulo keras.applications:

import numpy as np
from keras.applications.inception_resnet_v2 import (InceptionResNetV2,
                                                    preprocess_input,
                                                    decode_predictions)
from keras.preprocessing.image import load_img, img_to_array

target_shape = [299, 299, 3]

koala = img_to_array(load_img('koala.webp', target_size=target_shape))
# faz um conjunto contendo 1 imagem.
x = np.array([koala])
# processa x para as mesmas condições
# em que InceptionResNetV2 foi treinada.
x = preprocess_input(x)

model = InceptionResNetV2(weights='imagenet')
p = model.predict(x)
print(decode_predictions(p, top=3))

koala:  97.42%
wombat:  0.20%
maypole: 0.02%

InceptionResNetV2, treinada sobre o imagenet, sabe com bastante certa o que é um koala. :-)

Podemos utilizar os pesos treinados sobre o imagenet para iniciar um novo treinamento, em um processo conhecido como fine-tuning. No geral, isso nos leva à uma mais rápida convergencia. Neste caso, para acelerar as coisas aqui, eu congelei a atualização dos pesos de todo o pipeline conv, atualizando somente os pesos da última camada de decisão. Os resultados são comparáveis:

import keras
from keras import Model, Input, callbacks
from keras.applications import InceptionResNetV2
from keras.datasets import cifar10
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
from sklearn.model_selection import train_test_split

from sacred import Experiment

ex = Experiment('fine-tuning-inception-resnet-v2')


@ex.config
def my_config():
    epochs = 20
    batch_size = 256
    num_classes = 10
    valid_size = .25
    early_stopping_patience = 5
    optimizer = 'adam'
    ckpt = './weights.hdf5'


@ex.automain
def main(batch_size, num_classes, optimizer, epochs, valid_size, ckpt,
         early_stopping_patience):
    (x_train, y_train), (x_test, y_test) = cifar10.load_data()

    print('image shapes:', x_train.shape[1:])

    x_train = (x_train - x_train.mean(axis=0)) / x_train.std(axis=0)
    x_test = (x_test - x_test.mean(axis=0)) / x_test.std(axis=0)

    x_train, x_valid, y_train, y_valid = train_test_split(
        x_train, y_train, test_size=valid_size)

    x = Input(shape=x_train.shape[1:], name='inputs')
    model = InceptionResNetV2(input_tensor=x,
                              weights='imagenet',
                              include_top=False,
                              pooling='avg')
    model.trainable = False
    y = model.output
    y = Dense(num_classes, activation='softmax', name='predictions')(y)

    model = Model(inputs=x, outputs=y)
    model.compile(optimizer=optimizer,
                  loss='sparse_categorical_crossentropy',
                  metrics=['accuracy'])

    try:
        model.fit(x_train, y_train,
                  batch_size=batch_size,
                  epochs=epochs,
                  verbose=2,
                  validation_data=(x_valid, y_valid),
                  callbacks=[
                      callbacks.EarlyStopping(patience=early_stopping_patience),
                      callbacks.ModelCheckpoint(ckpt, save_best_only=True, verbose=True)
                  ])
    except KeyboardInterrupt:
        print('interrupted')
    else:
        print('done')

    print('reloading optimal weights...')
    model.load_weights(ckpt)

    score = model.evaluate(x_test, y_test, verbose=0)
    print('test loss:', score[0])
    print('test accuracy:', score[1])

WARNING - training-conv-network - No observers have been added to this run
INFO - training-conv-network - Running command 'main'
INFO - training-conv-network - Started
image shapes: (32, 32, 3)
Train on 37500 samples, validate on 12500 samples
Epoch 1/20
 - 122s - loss: 1.5673 - acc: 0.4115 - val_loss: 1.2524 - val_acc: 0.5470

Epoch 00001: val_loss improved from inf to 1.25245, saving model to ./weights.hdf5
Epoch 2/20
 - 116s - loss: 1.1259 - acc: 0.5957 - val_loss: 1.0814 - val_acc: 0.6135

Epoch 00002: val_loss improved from 1.25245 to 1.08137, saving model to ./weights.hdf5
Epoch 3/20
 - 117s - loss: 0.9420 - acc: 0.6645 - val_loss: 0.9103 - val_acc: 0.6778

Epoch 00003: val_loss improved from 1.08137 to 0.91025, saving model to ./weights.hdf5
Epoch 4/20
 - 122s - loss: 0.8101 - acc: 0.7122 - val_loss: 0.9491 - val_acc: 0.6679

Epoch 00004: val_loss did not improve
Epoch 5/20
 - 116s - loss: 0.6981 - acc: 0.7517 - val_loss: 0.8526 - val_acc: 0.7110

Epoch 00005: val_loss improved from 0.91025 to 0.85264, saving model to ./weights.hdf5
Epoch 6/20
 - 119s - loss: 0.6082 - acc: 0.7819 - val_loss: 0.8270 - val_acc: 0.7182

Epoch 00006: val_loss improved from 0.85264 to 0.82705, saving model to ./weights.hdf5
Epoch 7/20
 - 122s - loss: 0.5217 - acc: 0.8141 - val_loss: 0.8760 - val_acc: 0.7164

Epoch 00007: val_loss did not improve
Epoch 8/20
 - 121s - loss: 0.4371 - acc: 0.8441 - val_loss: 0.9056 - val_acc: 0.7227

Epoch 00008: val_loss did not improve
Epoch 9/20
 - 120s - loss: 0.3513 - acc: 0.8749 - val_loss: 1.0230 - val_acc: 0.7070

Epoch 00009: val_loss did not improve
Epoch 10/20
 - 119s - loss: 0.2744 - acc: 0.8998 - val_loss: 1.0952 - val_acc: 0.7116

Epoch 00010: val_loss did not improve
Epoch 11/20
 - 117s - loss: 0.2261 - acc: 0.9193 - val_loss: 1.1889 - val_acc: 0.7182

Epoch 00011: val_loss did not improve
done
reloading optimal weights...
test loss: 0.8398134949684143
test accuracy: 0.7196
INFO - training-conv-network - Completed after 0:22:10

Visualizando kernels

Pelas operações envolvidas em uma camada convolucional (hadamard, sum, add_bias e relu), uma “alta similaridade” entre o sinal de entrada e o padrão representado pelo kernel produzem altos valores de ativação. Em contrapartida, uma baixa similaridade produz uma ativação mais próxima ao 0.

Na primeira camada, o kernel efetivamente representa um padrão que será selecionado. Visualizar o que ativa nas camadas seguintes, entretanto, é um tanto problemático. Como um primeiro passo, podemos tentar olhar para a saída da convolução, que tente à remover os padrões que não se encaixam no definido pelo kernel:

import matplotlib
matplotlib.use('agg')
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from keras.engine import Model

observed_layer_names = ('activation_1', 'activation_2',
                        'activation_4', 'mixed_5b',
                        'mixed_6a', 'conv_7b')
observed_layer_outputs = [model.get_layer(name).output    
                          for name in observed_layer_names]
observer = Model(inputs=model.inputs, outputs=observed_layer_outputs)

z = observer.predict(x)
plot_kernels = 8

plt.figure(figsize=(12, 8))
gs1 = gridspec.GridSpec(len(z), plot_kernels)
gs1.update(wspace=0.025, hspace=0.05)

index = 0
for _z in z:
    print(_z.shape)
    kernels = _z.shape[-1]
    for k in range(plot_kernels):
        ax1 = plt.subplot(gs1[index])
        ax1.set_aspect('equal')
        ax1.axis('off')
        plt.imshow(_z[0, :, :, k])
        index += 1

plt.tight_layout()
plt.savefig('conv_outputs.webp')
plt.clf()

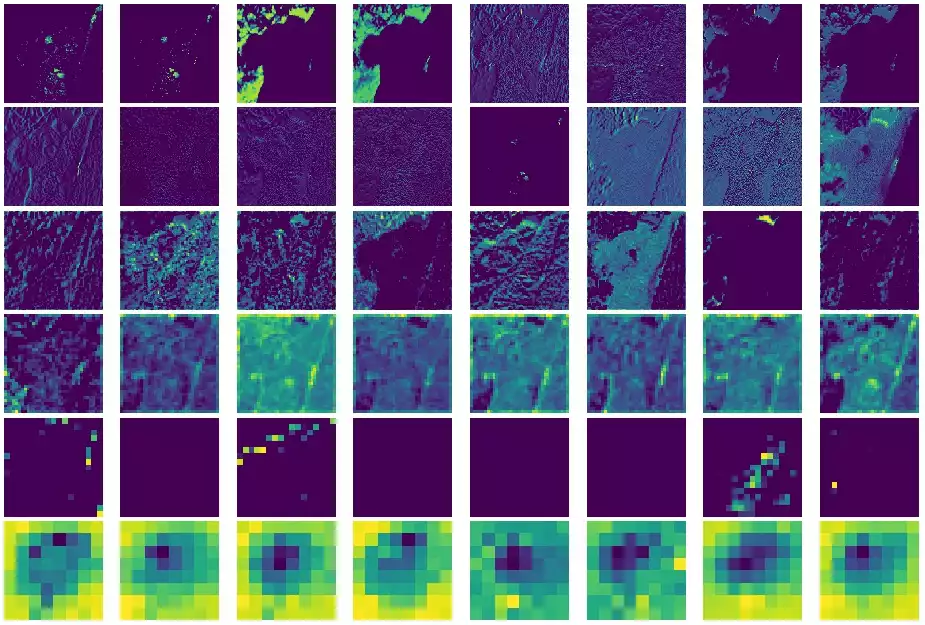
Visualização das saídas produzidas pelas camadas observadas, quando a rede é alimentada com o koala.

Apesar da InceptionResNetV2 ser bem maior que simplesmente 8 kernels de 6 camadas, podemos fazer algumas resalvas em relação às saídas:

Alguns kernels na primeira camada observada respondem com altas intensidades quando aplicados sobre o background claro.
Outros kernels, na terceira e quarta camadas, respondem ao koala em destaque.
O aprofundamento de uma rede — e sucessivas aplicações de poolling — reduz drasticamente a qualidade do sinal e dificulta a visualização. Entender uma rede profunda é definitivamente um desafio.

Melhores técnicas de visualização existem. Elas envolvem a otimização da imagens de entrada para uma unidade específica, retro-propagação de gradientes e oclusão.

Considerações finais

Neste post, eu descrevi alguns conceitos que compõem uma rede convolucional e apresentei alguns exemplos práticos em como utilizá-la. Em uma próxima oportunidade, eu vou mostrar como as convoluções podem ser utilizadas para processar padrões temporais e alguns novos modelos mais interessantes, como as redes recorrentes.